购买汽车基金及四年规划：实际应用分析

不是所有的最短路问题都涉及要找从源到目标地的最短行进距离，事实上，它们可能根本不涉及行进。因为边（或弧）可能代表了其他类型的活动，所以选择网络中的路和选择最佳的序列活动相对应。例如，表示边的“长度”的数字可能表示活动的成本，在这种情况下，该问题的目标就是确定使得这一系列活动的总成本最小。

下面是最短路问题应用的三种类型。

（1）行进的总距离最小，如里特城例子。

（2）一系列活动的总成本最小，如接下来的例子。

（3）一系列活动的总时间最小，如稍后的奎克公司例子。

1.使总成本最小的例子

莎拉刚刚高中毕业。在毕业典礼上，她的父母给了她21000 美元的汽车基金帮助她购买并保养一辆使用了三年的二手车，以供她上大学使用。由于开车费用和维修费用随着汽车的老化而飞速上涨，所以莎拉的父母告诉她在接下来的三个夏天里，她也可以一次或几次折价将她的汽车置换为其他使用了三年的二手车。如果她觉得这样做可以使她的总净成本最小，他们也会同意她这样做。他们还告诉莎拉，在四年后，他们会送她一辆新车作为大学毕业的礼物。所以，莎拉到那时肯定要计划把旧车折价卖出。

表6-2 给出了每一个时期莎拉购买一辆使用了三年的二手车的相关数据。例如，如果她两年后折价卖掉自己的车，那么在三年级时她就对下一辆车有1 年的所有权，其他情况以此类推。

表6-2　莎拉每个时期购买一辆使用了三年的二手车的数据　单位：美元

问在接下来的三个夏天里，莎拉什么时候应该折价卖掉她的汽车（如果有必要的话）可以使得她在大学四年里买车、开车、保养汽车的总费用最小？

图6-40 是把这个问题看作最短路问题的网络表述。其中，节点1，2，3 和4 分别代表莎拉上大学的第一年年末、第二年年末、第三年年末和第四年末；节点0 表示现在，上大学以前。从一个节点到另一个节点的每一条弧表示在第一个节点这个时间内买车，然后在第二个节点的那个时间把车折价卖出的费用。因为莎拉上大学以前开始买车，而在第四年年末又把车卖掉，所以节点0 是源，节点4 是目标地。

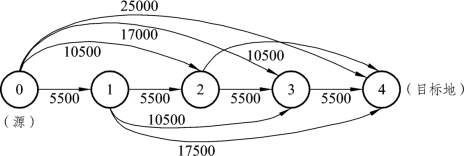
图6-40

若把莎拉什么时候应该折价购车看成一个最短路问题而对该问题所做的描述，那么节点的标号代表从现在开始计算的年份，每一条弧代表购车后又折价卖出的费用。

从源到目标地所选择的弧的数量表明莎拉将会多少次买车和折价卖车。例如，考虑下面这条路：

它表示现在开始购车，然后一年末把它折价卖掉去买第二辆车，接着在第三年年末又把第二辆车折价卖掉去买第三辆车，最后在第四年年末又把第三辆车折价卖出。

由于莎拉希望自己从现在（节点0）到第四年年末（节点4）的总费用最小，而对每一条弧的长度都需要计算买车、保养、折价买车的费用，所以

例如，我们来考虑从节点1 到节点3的弧。这条弧对应的是在第一年年末买车、使用和保养，然后在拥有了两年后把它折价卖掉的费用，所以

通过这种方法计算出来的弧长都标在图6-40中弧的旁边。将从节点0 到节点4的任意一条路的所有弧长加起来，就得到了在接下来的四年里制订旧车置换计划的总净费用。因此，通过寻求从源到目标地的最短路，我们将得到使得莎拉的总净费用最小的方案。

图6-41 给出了相应的电子表格模型。和图6-40 相比，除了原来的距离变成现在的费用以外，这两个模型是一样的。因此，目标单元格TotalCost（D23）给出的是最小总费用。图中可变单元格OnRoute（D12：D21）显示的最优解是通过点击Solver 按钮后得到的。由于数值1 表明了要经过的路径，所以最短路是：

在第二年年末把第一辆车折价卖掉；

在第四年年末把第二辆车折价卖掉。

这条路的长度为10500+10500=21000。所以，正如目标单元格所给出的结果，莎拉的总净费用为21000 美元。回想一下这个数额，它恰好等于莎拉的父母给莎拉提供的买车资金。(www.xing528.com)

将莎拉的问题作为最短路问题的电子表格模型，目标是使总成本而不是总距离最小。图的底部标出了目标单元格TotalCost（D23）和其他输出单元格Cost（E12：E21）以及NetFlow（H12：H16）的公式，其中可变单元格OnRoute（D12：D21）中的数值“1”表示通过Solver得到的最优解，显示这条最短（最便宜）路的总费用结果。

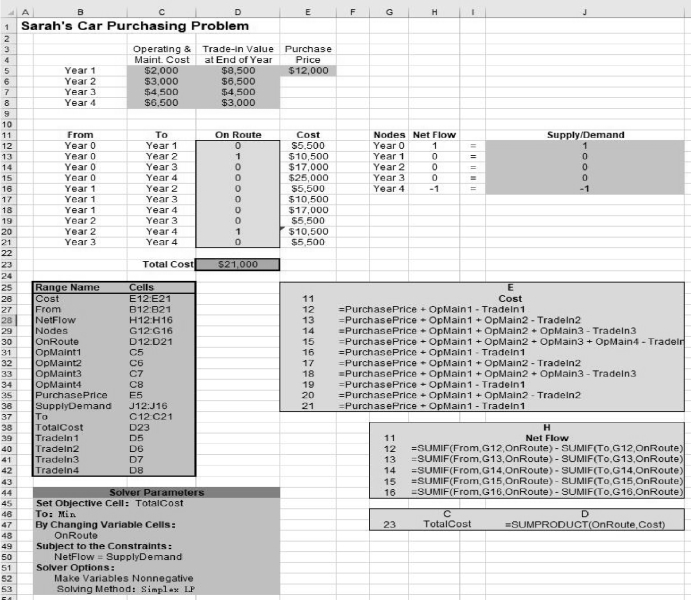
图6-41

2.使总时间最小化的例子

奎克（Quick）公司获悉了它的一个竞争对手计划将一种很有销售潜力的新产品投放市场。由于奎克公司也一直在研制一种类似的产品，并计划在20 个月后投放市场，然而，随着研究临近结束，奎克公司的管理者都希望迅速将产品推出去参与竞争。

现在还有四个没有时间重叠的阶段任务没有完成，包括正以正常速度进行剩下的研究工作（第一阶段）。然而，每个阶段的实施水平都可以从正常水平提高为优先水平或应急水平，使之能够加速完成，而且最后三个阶段中都可以考虑提高实施水平。第一阶段可以以正常速度也可以加速完成，表6-3 列出了在这些水平下所需要的时间。管理层现在已经给这四个阶段拨款3000 万美元，每个阶段的费用如表6-4 所示。

表6-3　准备奎克新产品的各阶段所需时间

表6-4　准备奎克新产品的各阶段费用　单位：万美元

管理层希望确定这四个阶段各自应该采取哪一种水平，从而在3000 万美元预算限制内，使得这种产品可以尽早推向市场。

图6-42 显示了将这个问题作为最短路问题的网络规划，其中，每一个节点代表那个时间点的情况；除了目标地以外，每个节点由两个数字表示。

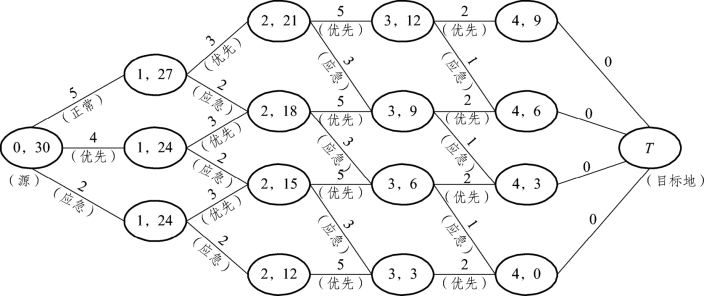
图6-42

将奎克公司的问题作为最短路问题的描述，除了虚拟目标地以外，弧的标签上第一个数字代表完成的阶段，第二个数字代表剩下阶段资金的剩余（单位：百万美元）；每条弧都给出了完成这个阶段所需要的时间（单位：月）。

源代表现在，即阶段0 已完成，还余下全部的3000 万美元的预算。每条弧代表那个阶段某一特定努力水平（在弧下的圆括号内注明）的选择，在这个努力水平下完成这个阶段所需要的时间（单位：月），用弧的长度（在弧的上方标明）表示。之所以选择时间作为弧长的尺度是因为目标是使得这四个阶段所花费的总时间最少。因此，把网络中某一条路的所有弧长加起来就得到了对应这条路的方案的总时间，网络中的最短路就是使得完成所有阶段的总时间最短的方案。

一旦四个节点中任一个节点标签的第一个数字为4，四个阶段的任务就完成了。那么为什么这个网络不是终结于这四个节点，而是又在每个节点又引出一条弧呢？因为最短路问题有且仅有一个目标地，所以，我们在右边加上了一个虚拟目标地。

因为指向虚拟目标地的每一条弧的长度都为0，对网络的这些改动不会影响从源到终点的总路长。

图6-43 显示了该问题的电子表格模型。它的格式和图6-39、图6-41 一样，除了在F 列和目标单元格TotalTime（D32）中涉及的数量是时间而不是距离或费用。在运行Solver 以后，可变单元格OnRoute（D4：D30）就会显示出哪些弧位于总时间最短的路上。因此，最短路为：

总长为2+3+3+2+0=10（月），如单元格TotalTime（D32）所示。完成这四个阶段任务的最终方案如表6-5 所示。虽然这个方案花费了总预算3000 万美元，但是它的确缩短了产品推向市场的时间，即从原来计划的20 个月缩短到仅仅10 个月。

表6-5　通过Excel Solver 软件获得的奎克最短路问题的最优解

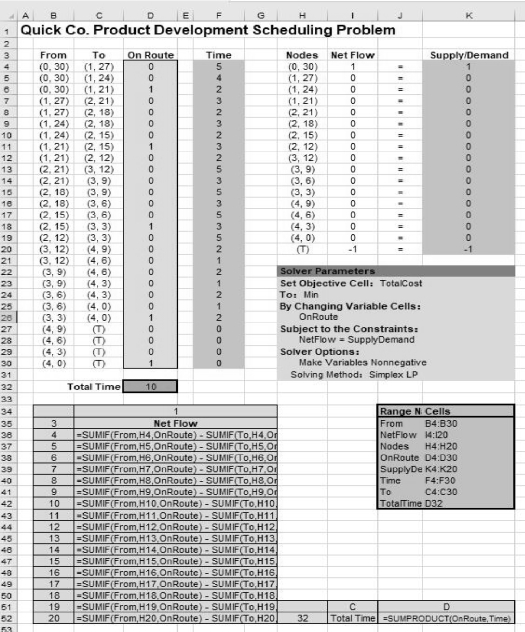
图6-43

将奎克公司问题作为最短路问题的电子表格模型，目标是使总时间最短，所以目标单元格为TotalTime（D32），其他输出单元格为NetFlow（I4：I20）；可变单元格OnRoute（D4：D30）的数值为“1”显示的是通过Solver 求解得到的最优解。

有了这些信息，奎克的管理者现在必须确定这个方案是否提供了最佳的时间-成本平衡决策依据。多花费几百万美元对总时间会有怎样的影响？稍微减少一些开支会有怎样的影响？通过迅速解决预算不是3000 万美元的最短路问题也会很容易为管理者提供这些信息。最终哪一个方案提供了最佳时间-成本平衡的决策只有管理者能够做出。