在各式各样的图中，有一类图是极其简单然但却是很有用的，这就是树。
例6-4 已知有五个城市，要在它们之间架设电话线，要求任何两个城市都可以互相通话（允许通过其他城市），并且电话线的根数最少。
用五个点 v1，v2，v3，v4，v5代表这五个城市，如果在某两个城市之间架设电话线，则在相应的两个点之间连一条边，这样一个电话线网就可以用一个图来表示。为了使任何两个城市都可以通话，这样的图必须是连通的。其次，若图中有圈的话，从圈上任意去掉一条边，余下的图仍是连通的，这样可以省去一根电话线。因而，满足要求的电话线网所对应的图必定是不含圈的连通图。图6-11 代表了满足要求的一个电话线网。
图6-11
定义1 一个无圈的连通图称为树。
例6-5 某工厂的组织机构如图6-12 所示。
图6-12
如果用图来表示，该工厂的组织机构图就是一个树（见图6-13）。
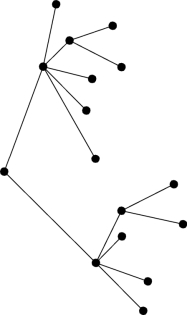
图6-13
下面介绍树的一些重要性质。
定理3 设图G=（V，E）是一个树，p（G）≥2，则G中至少有两个悬挂点。
证明 令P=（v1，v2，…，vk）是G中含边数最多的一条初等链，因 p（G）≥2，并且G 是连通的，故链P中至少有一条边，从而 v1与 vk是不同的。下面来证明：v1是悬挂点，即d（v1）=1。
用反证法。如果d（v1）≥2，则存在边[v1，vm]，使m≠2。若点 vm不在P 上，那么（vm，v1，v2，…，vk）是G中的一条初等链，它含的边数比P 多一条，这与P 是含边数最多的初等链矛盾。若点 vm在P 上，那么（v1，v2，…，vm，v1）是G中的一个圈，这与树的定义矛盾。于是必有d（v1）=1，即 v1是悬挂点。
同理可证，vk也是悬挂点，因而G 至少有两个悬挂点。
定理4 图G=（V，E）是一个树的充分必要条件是G 不含圈，且恰有p-1条边。
证明 必要性。设G 是一个树，根据定义，G 不含圈，故只要证明G 恰有p-1条边。对点数p 施行数学归纳法。
p=1，2时，结论显然成立。
假设当点数p≤n时，结论成立。设树G 含n+1个点，由定理3，G 含悬挂点。设 v1是G的一个悬挂点，考虑图
易见，
因
是n 个点的树，由归纳假设，
于是
(www.xing528.com)
充分性。只要证明G 是连通的即可，用反证法。设G 是不连通的，G 含s 个连通分图G1，G2，…，Gs（s≥2）。因每个 Gi（i=1，2，…，s）是连通的，并且不含圈，故每个 Gi是树。设 Gi有pi个点，则由必要性，Gi有pi-1条边，于是
这与 q（G）=p（G）-1的假设矛盾。
定理5 图G=（V，E）是一个树的充分必要条件是G 是连通图，并且 q（G）=p（G）-1。
证明 必要性。设G 是树，根据定义，G 是连通图，由定理4，q（G）=p（G）-1。
充分性。只要证明G 不含圈，对点数施行归纳法。
当 p（G）=1，2时，结论显然成立。
设 p（G）=n（n≥1）时结论成立。现设 p（G）=n+1，首先证明G 必有悬挂点。若不然，因G是连通的，且 p（G）≥2，故对每个点 vi，有 d（vi）≥2。从而
这与 q（G）=p（G）-1矛盾，故G 必有悬挂点。设 v1是G的一个悬挂点，考虑G-v1，这个图仍是连通的，
由归纳假设知，G-v1不含圈，于是G 也不含圈。
定理6 图G 是树的充分必要条件是任意两个顶点之间恰有一条链。
证明 必要性。因G 是连通的，故任两个点之间至少有一条链。但如果某两个点之间有两条链的话，那么图G中含有圈，这与树的定义矛盾，从而任两个点之间恰有一条链。
充分性。设图G中任两个点之间恰有一条链，那么易见G 是连通的。如果G中含有圈，那么这个圈上的两个顶点之间有两条链，这与假设矛盾，故G 不含圈，于是G 是树。
由这个定理很容易推出如下结论：
（1）从一个树中去掉任意一条边，则余下的图是不连通的。由此可知，在点集合相同的所有图中，树是含边数最少的连通图。这样，例6-4中所要求的电话线网就是以这五个城市为点的一个树。
（2）在树中不相邻的两个点间添上一条边，恰好得到一个圈。进一步说，如果再从这个圈上任意去掉一条边，可以得到一个树。
在图6-11中，添加边[v2，v1]，就得到一个圈（v1，v2，v5，v1），如果从这个圈中去掉一条边[v1，v5]，就得到图6-14 所示的树。
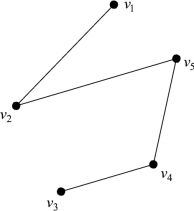
图6-14
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
