【摘要】:约束条件:① 卡车载重10 t:0.2x1+0.4x2+0.3x3+0.2x4≤10;② 装载体积12 m3:0.3x1+0.5x2+0.4x3+0.3x4≤12;③ 每种货物最多装8 件:xi≤8,i=1,2,3,4;④ 非负且为整数:xi≥0且为整数。数学模型:根据上面的分析,即得到如下数学模型:2.应用Excel 求解利用Excel 求解的结果如图5-8 所示,其结果为每种货物均装载八件时,可使得所携带货物的总价值最大,为17.2 万元。图5-8多维背包问题的Excel 电子模型
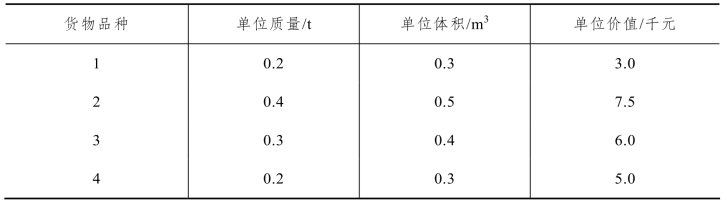
现有一辆载重为10 t,装载体积为12 m3的卡车,可装载四种货物,已知每种货物各八件,其他有关信息如表5-2 所示。试求携带货物价值最大的装载方案。
表5-2 四种货物的单位质量、体积及价值
1.建模
关于动态规划的分析从略,直接进行建模。
(1)决策变量:
设卡车装载编号为i的货物数量为xi,i=1,2,3,4。
(2)约束条件:
① 卡车载重10 t:0.2x1+0.4x2+0.3x3+0.2x4≤10;
② 装载体积12 m3:0.3x1+0.5x2+0.4x3+0.3x4≤12;
③ 每种货物最多装8 件:xi≤8,i=1,2,3,4;(https://www.xing528.com)
④ 非负且为整数:xi≥0且为整数。
对于问题2,还需要增加条件:x1,x2≥1。
(3)目标函数:
使卡车装载货物的总价值最大:maxz=3x1+7.5x2+6x3+5x4。
(4)数学模型:
根据上面的分析,即得到如下数学模型(整数线性规划):
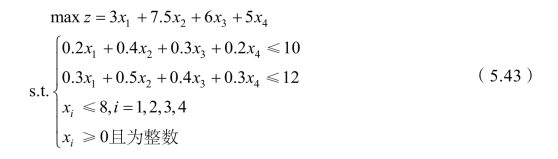
2.应用Excel 求解
利用Excel 求解的结果如图5-8 所示,其结果为每种货物均装载八件时,可使得所携带货物的总价值最大,为17.2 万元。此时,总装载体积为12 m3,总装载质量为8.8 t。

图5-8 多维背包问题的Excel 电子模型
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




