动态规划的最优性原理和最优性定理

20 世纪50 年代，R.Bellman 等人通过研究一类多阶段决策问题，提出了最优性原理（有的翻译成最优化原理），并将之作为动态规划的理论基础，用来解决许多决策过程的优化问题。长期以来，许多有关动态规划的著作都用“依据最优化原理，则有……”的提法来处理决策过程的优化问题。然而，人们对用这样的一个简单的原理作为动态规划方法的理论根据很难理解。的确如此，实际上，此提法是给用动态规划方法处理决策过程的优化问题披上了一层神秘的色彩，使读者不能正确地理解动态规划方法的本质。

下面将介绍“动态规划的最优性原理”的原文含义，指出它为什么不是动态规划的理论基础，进而揭示动态规划方法的本质，指出其理论基础是“最优性定理”。

动态规划的最优性原理：“作为整个过程的最优策略应具有这样的性质，即无论过去的状态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略。”简言之，一个最优策略的子策略总是最优的。

但是，随着人们对动态规划研究的深入，逐渐认识到：基于不同类型的问题所建立的严格定义的动态规划模型，必须用相应的最优性原理给以必要的验证。也就是说，最优性原理不是对任何决策过程都普遍成立的，而且“最优性原理”与动态规划基本方程，并不是无条件等价的，两者之间也不存在确定的蕴含关系。可见，动态规划的基本方程在动态规划的理论和方法中起着非常重要的作用，而反映动态规划基本方程的是最优性定理，它是策略最优性的充分必要条件；而最优性原理仅仅是策略最优性的必要条件，是最优性定理的推论，在求解最优策略时，更需要的是其充分条件。所以，动态规划的基本方程或者说最优性定理才是动态规划的理论基础。

定理 1（动态规划的最优性定理） 设阶段数为n的多阶段决策过程，其阶段编号为k=0，1，…，n-1，允许策略为其最优策略的充要条件是对任意一个k（0＜ k ＜ n-1）和 s0∈S0，有

式中它是由给定的初始状态 s0和子策略 p0，k-1所确定的k 段状态。当V 是效益函数时，opt 取max；当V 是损失函数时，opt 取min。

证明　必要性。设是最优策略，则

但对于从k 至n-1阶段的子过程而言，它的总指标取决于过程的起始点和子策略pk，n-1，而这个起始点是由前一段子过程在子策略 p0，k-1下确定的。因此，在策略集合P0，n-1上求最优解，就等价于先在子策略集合上求最优解，然后再求这些子最优解在子策略集合 p0，k-1（s0）上的最优解。故上式可写为(www.xing528.com)

在这里记号“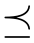”的含义是：当 opt 表示 max 时就表示“≤”；当opt 表示min 时就表示“≥”。因此，式（5.32）为

推论　若允许策略是最优策略，则对任意的k，0＜ k ＜ n-1，它的子策略对于以为起点的k 到n-1子过程来说，必是最优策略。（注意：k 阶段状态是由 s0和所确定的）

证明　用反证法。若不是最优策略，则有

此处记号“≺”是：当opt 表示max 时表示“＜”，当opt 表示min 时表示“＞”。因而

故与以上定理的必要性矛盾。证毕。

此推论就是前面提到的动态规划的“最优性原理”，它仅仅是最优策略的必要性。从最优性定理可以看到：如果一个决策问题有最优策略，则该问题的最优值函数一定可用动态规划的基本方程来表示，反之亦真。也就是说，该定理为人们用动态规划方法来处理决策问题提供了理论依据并指出了方法，即要充分分析决策问题的结构，使它满足动态规划的条件，以便正确地写出动态规划的基本方程。