动态规划方法的基本思想与方程式

现在，再结合解决最短路线问题来介绍动态规划方法的基本思想。生活中的常识告诉我们，最短路线有一个重要特性：如果由起点A 经过P 点和H 点而到达终点G 是一条最短路线，则由点P 出发经过点H 而到达终点G的这条子路线，对于从点P 出发到达终点的所有可能选择的不同路线来说，必定也是最短路线。例如，在最短路线问题中，若找到了A →B1→C2→D1→E2→F2→G 是由A 到G的最短路线，则 D1→E2→F2→G应该是由 D1出发到G 点的所有可能选择的不同路线中的最短路线。此特性用反证法易证。因为如果不是这样，则从P 点到G 点有另一条距离更短的路线存在，把它和原来最短路线中由A 点到达P点的那部分连接起来，就会得到一条由A 点到G 点的新路线，它比原来那条最短路线的距离还要短些。这与假设矛盾，是不可能的。

根据最短路线这一特性，寻找最短路线的方法，就是从最后一段开始，用由后向前逐步递推的方法，求出各点到G 点的最短路线，最后求得由A 点到G 点的最短路线。所以，动态规划的方法就是从终点逐段向始点方向寻找最短路线的一种方法，如图5-3 所示。

图5-3

下面按照动态规划的方法，将例5-1中从最后一段开始计算，由后向前逐步推移至A 点。

当k=6时，由 F1到终点G 只有一条路线，故 f6（F1）=4。同理，f6（F2）=3。

当k=5时，出发点有 E1，E2，E3三个。若从 E1出发，有两个选择：①至 F1；②至 F2，则

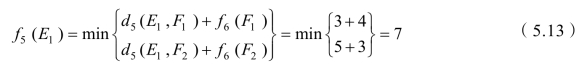
其相应的决策为u5（E1）=F1。

这说明，由 E1至终点G的最短距离为7，其最短路线是

同理，从 E2和 E3出发，有

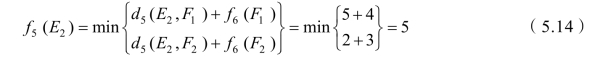
其相应的决策为u5（E2）=F2。

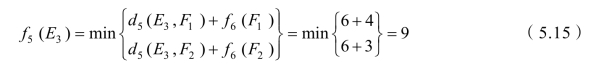
且 u5（E3）=F2。

类似地，可算得

当k=4时，有

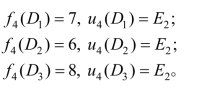
当k=3时，有

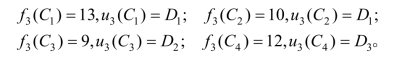
当k=2时，有

当k=1时，出发点只有一个A 点，则

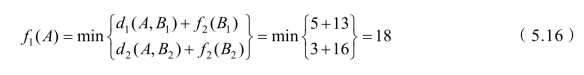
且 u1（A）=B1。

于是得到从起点A 到终点G的最短距离为18。为了找出最短路线，再按计算的顺序反推之，可求出最优决策函数序列{uk}，即由

组成一个最优策略。因而，找出相应的最短路线为

从上面的计算过程可以看出，在求解的各个阶段，我们利用了k 阶段与k+1阶段之间的递推关系：

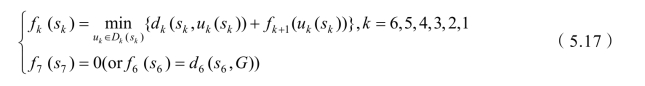
一般情况，k 阶段与k+1阶段的递推关系式可写为

边界条件为

这种递推关系式（5.18）称为动态规划的基本方程。

现在把动态规划方法的基本思想归纳如下：

（1）动态规划方法的关键在于正确地写出基本的递推关系式和恰当的边界条件（简言之为基本方程）。要做到这一点，必须先将问题的过程分成几个相互联系的阶段，恰当地选取状态变量和决策变量并定义最优值函数，从而把一个大问题化成一族同类型的子问题，然后逐个求解。即从边界条件开始，逐段递推寻优，在每一个子问题的求解中，均利用了它前面的子问题的最优化结果，依次进行，最后一个子问题所得的最优解，就是整个问题的最优解。

（2）在多阶段决策过程中，动态规划方法是既把当前一段和未来各段分开，又把当前效益和未来效益结合起来考虑的一种最优化方法。因此，每段决策的选取是从全局来考虑的，与该段的最优答案选择一般是不同的。

（3）在求整个问题的最优策略时，由于初始状态是已知的，而每段的决策都是该段状态的函数，故最优策略所经过的各段状态便可逐次变换得到，从而确定最优路线。如例5-1中的最短路线问题，初始状态A 已知，则按下面箭头所指的方向逐次变换有

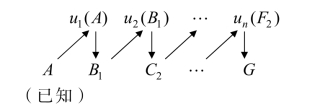
从而可得最优策略为{u1（A），u2（B1），…，un（F2）}，相应的最短路线为

(www.xing528.com)

上述最短路线问题的计算过程，也可借助图形直观简明地表示出来，如图5-4 所示。

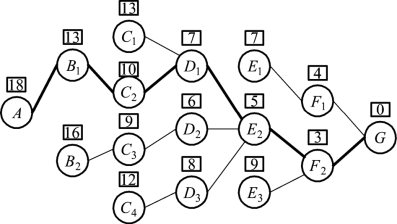
图5-4

在图5-4中，每节点处上方方格内的数，表示该点到终点G的最短距离。用直线连接的点表示该点到终点G的最短路线，未用直线连接的点则说明它不是该点到终点G的最短路线，故这些支路均被舍去了。图中粗线表示由始点A 到终点G的最短路线。

这种在图上直接作业的方法叫做标号法。如果规定从A 点到G 点为顺行方向，则由G 点到A 点为逆行方向，那么，图5-4 是由G 点开始从后向前标的。这种以A 为始端，G 为终端，从G 到A的解法称为逆序解法。

由于线路网络的两端都是固定的，且线路上的数字表示两点间的距离，则计算从A 点到G 点和计算从G 点到A 点的最短路线的距离是相同的，因而，标号也可以由A 开始，从前向后标。只是此时要视G 为起点，A 为终点，按动态规划方法处理，如图5-5 所示。

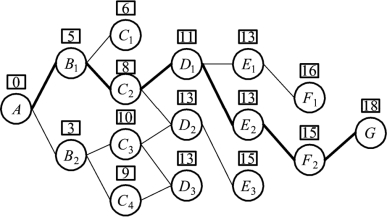
图5-5

图5-5中，每节点处上方方格内的数表示该点到A 点的最短距离，用直线连接的点表示该点到起点A的最短路线，粗线表示A 点到G 点的最短路线。这种以G 为始端、A 为终端的从A 到G的解法称为顺序解法。

由此可见，顺序解法和逆序解法只是表示行进方向的不同或对始端、终端看法的颠倒。但用动态规划方法求最优解时，都是在行进方向规定后，均要逆着这个规定的行进方向，从最后一段向前逆推计算，逐段找出最优途径。

从上面例5-1的计算过程可以看到，动态规划的方法与穷举法相比有以下两个优点：

（1）减少了计算量。计算例5-1 时若用穷举法，就要对48 条线路的长度进行比较，运算在计算机上进行时，比较运算要进行47 次；求各条线路的距离，既要使用逐段累加方法，也要进行6+12+24+48+48=138 次加法运算。而用动态规划方法来计算，比较运算（从k=5段开始向前算）共进行3+3+4+4+1=15 次；每次比较运算相应地有两次加法运算，再去掉中间重复的两次（即 B1→C1，B2→C4各多算了一次），实际上只有28 次加法运算。可见，动态规划方法比穷举法减少了计算量，而且随着段数的增加，计算量将大大减少。

（2）丰富了计算结果。在逆序（或顺序）解法中，我们得到的不仅仅是由A 点（或G 点）出发到G 点（或A 点）的最短线路及相应的最短距离，而且得到了从所有各中间点出发到G点（或A 点）的最短线路及相应的距离。这就是说，求出的不是一个最优策略，而是一族最优策略。这对许多实际问题来讲是很有用的，有利于帮助分析所得结果。

在明确了动态规划的基本概念和基本思想之后，我们看到，给一个实际问题建立动态规划模型时，必须做到以下五点：

（1）将问题的过程划分成恰当的阶段。

（2）正确选择状态变量 sk，使它既能描述过程的演变，又要满足无后效性。

（3）确定决策变量 uk及每阶段的允许决策集合 Dk（sk）。

（4）正确写出状态转移方程。

（5）正确写出指标函数Vk，n的关系，它应满足下面三个性质：

① 是定义在全过程和所有后部子过程上的数量函数。

② 要具有可分离性，并满足递推关系。即

③ 函数ψk（sk，uk，Vk+1，n）对于变量Vk+1，n要严格单调。

以上五点是构造动态规划模型的基础，是正确写出动态规划基本方程的基本要素。而一个问题的动态规划模型是否能够正确给出，这集中地反映在能否恰当地定义最优值函数和正确地写出递推关系式及边界条件上。简言之，要正确写出动态规划的基本方程。

由于动态规划方法有逆序解法和顺序解法之分，那么，它们的动态规划基本方程应如何来表述呢？下面先给出动态规划逆序解法的基本方法。

设指标函数是取各阶段指标的和的形式，即

其中 vj（sj，uj）表示第j 段的指标。它显然满足指标函数的三个性质，所以上式可写成

当初始状态给定时，过程的策略就被确定，那么指标函数也就确定了。因此，指标函数是初始状态和策略的函数，可记为Vk，n[sk，pk，n（sk）]。故上面递推关系又可写成

其子策略pk，n（sk）可看成由决策 uk（sk）和pk+1，n（sk+1）组合而成。即

如果用表示初始状态为sk的后部子过程所有子策略中的最优子策略，则最优值函数为

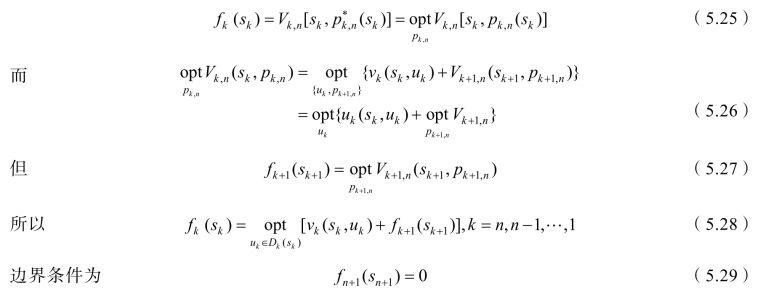
这就是动态规划逆序解法的基本方程，式中

其求解过程是：根据边界条件，从k=n开始，由后向前逆推，从而逐步可求得各段的最优决策和相应的最优值，最后求出 f1（s1）时，就得到整个问题的最优解。

关于动态规划顺序解法的基本方程，应如何表述呢？假定阶段序数k 和状态变量 sk的定义不变，而改变决策变量 uk的定义，如例5-1中取uk（sk+1）=sk，则这时的状态转移不是由 sk，uk来确定sk+1，而是反过来由sk+1，uk来确定 sk，则状态转移方程的一般形式为

因而，第k 阶段的允许决策集合也应做相应的改变，记为指标函数也应换成以sk+1和 uk的函数表示，于是可得动态规划顺序解法的基本方程：

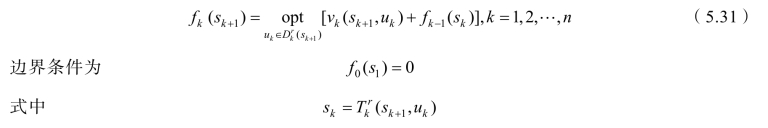
其求解过程是：根据边界条件，从k=1开始，由前向后顺推，逐步求得各段的最优决策和相应的最优值，最后求出fn（sn+1），就得到整个问题的最优解。