0-1整数规划模型及其应用

0-1 整数规划是整数规划的特殊情形，也是应用非常广泛的一类整数规划。在0-1 整数规划中，其整数变量只能取0 或1，通常用这些0-1 变量来表示某种逻辑关系。例如，用“1”表示“是”，用“0”表示“非”。

下面看一个选址问题。由于对每一个备选点都有“选”或“不选”两种方案，因此可以引入0-1 型决策变量来构建数学模型。

例4-4　某公司计划在m 个地点建厂，可供选择的地点有 A1，A2，…，Am，它们的生产能力分别是 a1，a2，…，am（假设生产同一产品）；第i 个工厂的建设费用为fi（i=1，2，…，m）。又有n个地点 B1，B2，…，Bn需要销售这种产品，其销量分别为b1，b2，…，bn。从工厂运往销售地的单位运费为cij。试决定应在哪些地方建厂，既能满足各地需要，又使总建设费用和总运输费用最省？（仅给出求解模型）

解　设决策变量 xij表示从工厂i 到销地j的运输量，yi表示是否在i 地建厂（yi=1表示在i 地建厂；yi=0表示不在i 地建厂），则可建立数学模型如下：

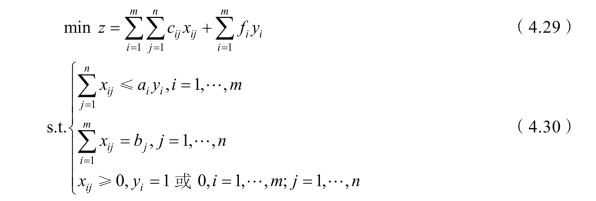
对于0-1 整数规划的求解，一般有完全枚举法和隐枚举法两种。完全枚举法就是检查每个0-1 变量等于0 或1的所有组合，满足所有约束条件并使目标函数值取得最优的组合就是0-1 整数规划的最优解。如果0-1 变量有n 个，就需要检查2n个变量组合。而当n＞15时，这几乎是不可能的，因此人们进一步提出了隐枚举法（implicit enumeration）。隐枚举法只需要检查全部变量组合中的一部分就可求出最优解，大大减少了计算量。比如，在2n个变量组合中，往往只有一部分是可行解，当发现某个变量组合不满足其中一个约束条件时，就不必再检查其他约束条件是否可行；并且对于可行解，其目标函数值也有优劣之分。若已发现一个可行解，则可根据其目标函数值构造一个过滤条件，对于目标函数值比它差的变量组合就不必再检查可行性了；当遇到目标函数值更优的可行解时，则更新过滤条件。这些做法都可以减少运算次数，使最优解能较快地被发现。

例4-5　求解下列0-1 整数规划问题：(www.xing528.com)

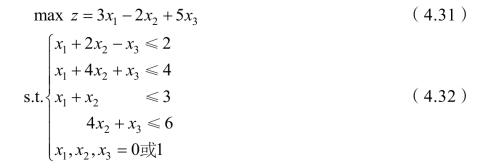
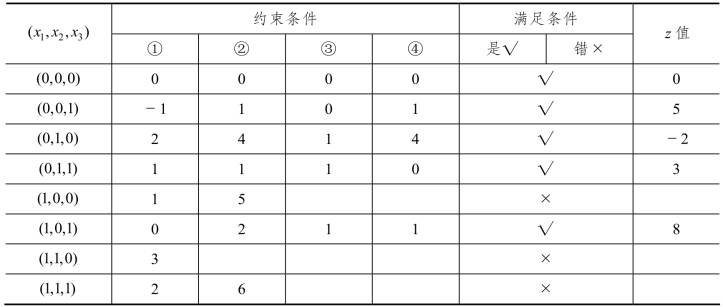
解　若用完全枚举法来求解，则需要将所有的0-1 变量组合找出。本例中有 23=8种情况（见表4-6），其中，使目标函数值达到最优的组合就是最优解。从表中可以看出，该问题的最优解为x*=（1，0，1）T。

表4-6　0-1 规划问题求解（一）

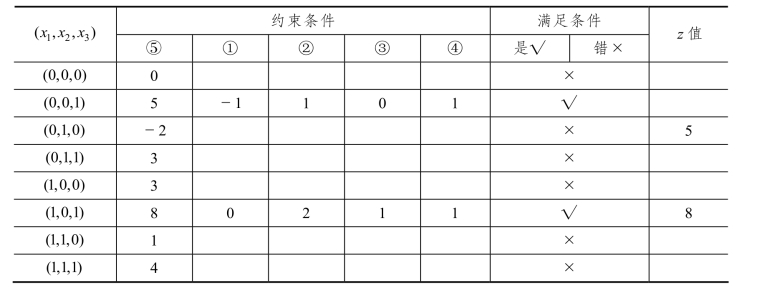
如上所述，完全枚举法的工作量相当大，而隐枚举法则是通过加入一定的条件，减少计算量，从而较快地求得最优解。在本例中，首先可以看出，x1=0，x2=0，x3=1是一个可行解，目标函数值为5。于是将3x1-2x2+5x3≥5设为一个过滤条件，凡是目标函数值小于5的变量组合都不必讨论，如表4-7 所示。当检验到 x1=1，x2=0，x3=1时，这是一个目标函数值大于5的可行变量组合，于是更新过滤条件为3x1-2x2+5x3≥8。如此继续，直到检验所有变量组合，可得最优解就是 x*=（1，0，1）T。虽然这里也检验了每一个0-1 组合，但是计算量却小于不加过滤条件的完全枚举法。

表4-7　0-1 规划问题求解（二）