割平面法用于整数规划问题的线性约束求解

割平面法是Gomory 于1958 年提出来的，它的基本思想是：在与整数规划问题相对应的线性规划问题中依次引进线性约束条件，使问题的可行域逐步缩小。在求解过程中，首先不考虑变量 xi是整数这一条件，增加的线性约束条件使原可行域切掉一部分，切掉的部分中只包含非整数解。这个方法的关键是怎样找到适当的割平面，以满足使可行域缩小又不切掉整数解的条件。

下面以实例说明割平面法的求解过程。

例4-3　求解下列规划问题：

解　首先不考虑整数约束，用单纯形法求解相应的线性规划问题B，得最终单纯形表，如表4-2 所示：

表4-2

将系数和常数项分解成整数和非负真分式之和，上式化为；

移项后得：

现考虑整数条件，由于 x1，x2为非负整数，由条件④知 x3，x4也为非负整数。在上式中左边为整数，右边（·）为正数，要使等式成立，等式右边必须小于等于零，也就是，整数约束条件可由下式来代替：

这就是切割方程，将它作为约束条件，加到相应线性规划B中，得到问题 B1。

图4-5

从图4-5中可见，切割方程只割去相应线性规划问题可行域的部分非整数解，原来的整数解全部保留。

对该模型 B1不需要重新求解，只要把增加的约束条件加到问题B的最优单纯形表中即可（见表4-3）。

表4-3

这时得到的为非可行解，用对偶单纯形法进行求解。

选择x5作为换出变量，

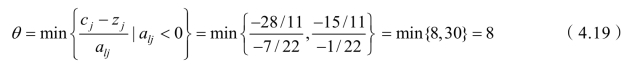
所以 x3作为换入变量，进行迭代，如表4-4 所示。

表4-4(www.xing528.com)

由计算结果知，还没有得到整数解，重新再寻找割平面方程。

由 x1行得：

将系数和常数项分解成整数和非负真分数之和：

移项得：

得到新的约束条件：

在 B1的最优单纯形表中加上此约束，用对偶单纯形法求解，如表4-5 所示。

表4-5

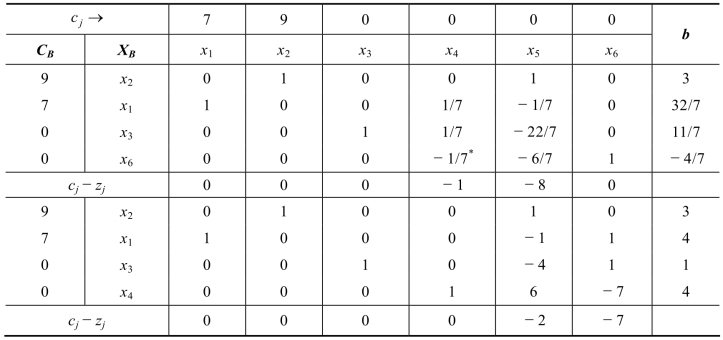
则最优解为最优目标函数值为z*=55。

由上例求解过程，归纳割平面法求解步骤如下：

第一步：不考虑整数约束，求相应线性规划模型B的最优解。若最优解恰为整数，则停止计算；若最优解不为整数，进入第二步。

第二步：寻找割平面方程。

（1）令 xi为相应线性规划最优解中不符合整数条件的一个基变量，由单纯形表的最终表得到：

（2）将 bi和 aik都分解成整数部分N 与非负真分数f 之和：

其中N 表示不超过b的最大整数。如b=3.30，则N=3，f=0.30；b=-1.23，则N=-2，f=0.77。

将 bi，aik代入得到：

（3）得到割平面方程：

第三步：把割平面方程加入相应线性规划B的最终单纯形表中，用对偶单纯形法求解。若解为非负整数解，则停止计算，得到最优整数解；若得到的解不是非负整数解，重复第二步过程，重新计算。