分枝定界法解决整数规划问题

在线性规划中，变量 xj是在一个连续范围内取值的，因此可行解的个数为无限多个。而在整数规划中，变量只能取离散的整数值，可行解的数量是有限的。从有限多的可行解中寻找最优解，最笨的也是最简单的想法就是枚举法，即把问题的解全部列举出来，进行比较，从而找到最优解。但对于一般整数规划问题来说，可行解的总数随变量的增长成指数倍增长，使枚举法失去意义。此时，分枝定界法（brach and bound method）的提出解决了整数规划的求解问题。

分枝定界法是20 世纪60 年代初由Land Doig 和Dakin 等人提出的，它适用于解纯整数或混合整数规划问题。其求解步骤如下：

第一步：令整数规划模型为A，首先不考虑整数约束条件，求相应线性规划模型B的最优解。若B 没有可行解，则A 也没有可行解，计算结束；若B 有最优解且符合A中的整数约束条件，则B的最优解为A的最优解，计算结束；若B 有最优解，但不符合A的整数约束条件，转第二步进行计算。

第二步：用观察法找A中的一个整数可行解，一般取xj=0（j=1，2，…，n）试探，求得目标函数值作为下界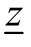；不考虑整数约束条件得到的B 模型的最优目标函数值作为上界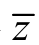，使整数规划A的最优目标函数值 z*符合以下条件：

第三步：分枝。在B的最优解中任选一个不符合整数条件的变量 xj，令 xj＝bj，以[bj]表示小于 bj的最大整数，构造两个约束条件：

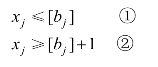
将这两个约束条件分别加入问题B，得到两个后继问题 B1和 B2，不考虑整数约束条件求解这两个后继问题。

第四步：定界。以每个后继问题为一分枝标明求解的结果，并与其他问题的解进行比较，找出分枝中最优目标函数值的最大者作为新的上界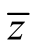；再从已符合整数条件的各分枝中，找出目标函数值的最大者作为新的下界，若无整数解，则取

第五步：比较与剪枝。各分枝的最优目标函数中，若有小于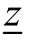者或无可行解者，则剪掉这枝（用打×表示），即以后不再考虑了；若有大于z 者，且不符合整数条件，则重复第三步，一直到得到为止，得最优整数解 x*。

例4-2　用分枝定界法求解纯整数规划问题：

解　首先不考虑整数约束④，得到相应的线性规划问题B：

用单纯形法进行求解，得到最优解：x1＝3.25，x2＝2.5，max z＝14.75。这时上界z=14.75，下界

由于 x1＝3.25，x2＝2.5为非整数解，取 x2＝2.5构造两个分枝。由［2.5］＝2，则两个分枝为：x2≤2，x2≥3，分别加到B中构成两个后继问题 B1，B2：(www.xing528.com)

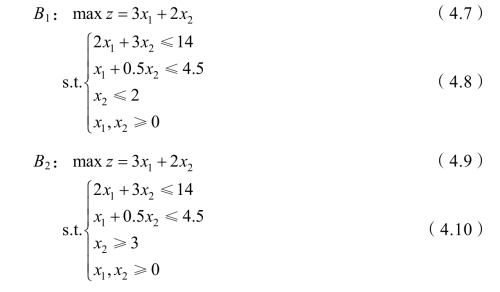
如图4-2 所示，即把原来的可行域分为两部分，把中间没有整数解的部分切割掉，缩小搜索范围。

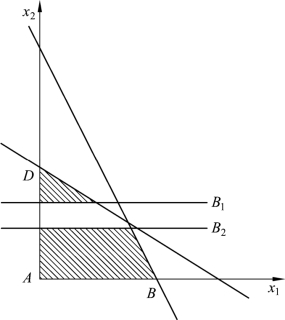
图4-2

对 B1，B2求解，B1的最优解为：x1＝3.5，x2＝2，max z＝14.5；B2的最优解为：x1＝2.5，x2＝3，max z＝13.5。

B1，B2仍没有满足整数条件，需要继续分枝，这时的下界依然为上界为对 B1继续分枝。 B1中只有 x1为非整数，取 x1＝3.5进行分枝，构造两个约束分别为：x1≤3，x1≥4，得到两个新的分枝 B11，B12：

其可行域如图4-3 所示。对 B11进行求解，得 x1=3，x2=2，maxz=13；B12的最优解为x1=4，x2=1，maxz=14。

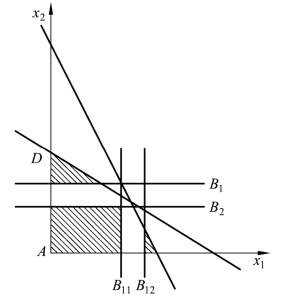
图4-3

这时得到的满足整数约束条件的新的目标函数值为14，大于 B2分枝的目标函数值，因此分枝 B2不需要再分枝了。这时下界为上界为因此该整数规划的最优解为x1＝4，x2＝1，max z＝14。

分枝定界法的过程如图4-4 所示：

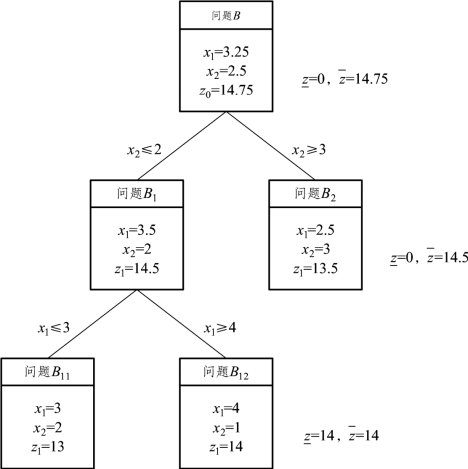
图4-4