问题提出：设备数量约束条件下的线性规划最优解

在线性规划模型中，得到的最优解往往是分数或小数，但有些实际问题中要求有的解必须是整数，如机器设备的台数、人员的数量等，这就要在原来线性规划模型的基础上产生一个新的约束，即要求变量中某些或全部为整数，这样的线性规划称为整数规划（integer programming），简称为IP。它是规划论中的一个分枝。

整数规划是一类特殊的线性规划。为了满足整数解的条件，初看起来，只要对相应线性规划的非整数解四舍五入取整就可以了，但是当变量取值很大时，用上述方法得到的解与最优解差别不大；而当变量取值较小时，得到的解与实际最优解差别较大；当变量较多时，如n=10个，则整数组合有210＝1024 个，而且整数解不一定在这些组合当中。先看下面的例子。

例4-1　某工厂生产甲、乙两种设备，已知生产这两种设备需要消耗材料A 和材料B，有关数据如表4-1 所示。问这两种设备各生产多少才使工厂利润最大？

表4-1

解　设生产甲、乙这两种设备的数量分别为x1，x2，由于是设备台数，则其变量都要求为整数，建立模型如下：

(www.xing528.com)

求该模型的解，先不考虑整数约束条件④。用单纯形法对相应线性规划求解，其最优解为：x1＝3.25，x2＝2.5，max z＝14.75。

由于 x1＝3.25，x2＝2.5都不是整数，不符合整数约束条件，那么用四舍五入取整或凑整的办法能得到最优解吗？

取 x1＝4，x2＝2代入约束条件，破坏了约束②；取 x1＝3，x2＝2代入约束条件，满足要求，此时 z＝13，但这不是最优解，因为x1＝4，x2＝1时，z＝14。

由此可知，用这种四舍五入取整或凑整的方法找不到最优解。下面再用图解方法来看寻找整数解的过程。

图4-1中，ABCD 为相应线性规划的可行域，可行域中两个数字均为整数的点为可行的整数解，而凑整得到的（4，2）不在可行域范围内，（3，2）点尽管在可行域内，但没有使目标达到极大值。为了使目标函数达到极大值，可使目标函数等值线向原点方向移动，直到遇到点（4，1）为止，此时z＝14。

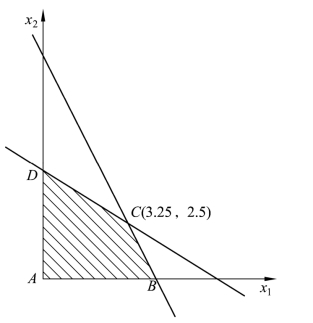
图4-1