【摘要】：在物流管理中，经常碰到大宗物资的运输问题。这类问题可用如下数学语言描述。，n，其需要量分别为bj；从 Ai到Bj运输单位物资的运价（单价）为cij。表3-1产销平衡表表3-2单位运价表若用 xij表示从 Ai到Bj的运量，那么在产销平衡的条件下，要求得总运费成本最小的调运方案，可求解以下数学模型：这就是运输问题的数学模型。即对于产销平衡的运输问题，由于有以下关系式存在：所以模型最多只有m+n-1个独立约束方程，即系数矩阵的秩≤m+n-1。
在物流管理中，经常碰到大宗物资的运输问题。如煤、钢铁、木材、粮食等物资，在全国有若干生产基地，根据已有的交通网，应如何制订调运方案，将这些物资运到各消费地点，而使总运输成本最小。这类问题可用如下数学语言描述。
已知有m 个产地 Ai，i=1，2，…，m，可供应某种物资，其供应量（产量）分别为ai；有n 个销地Bj，j=1，2，…，n，其需要量分别为bj；从 Ai到Bj运输单位物资的运价（单价）为cij。将这些数据汇总于产销平衡表和单位运价表中，如表3-1 和表3-2 所示。
表3-1 产销平衡表
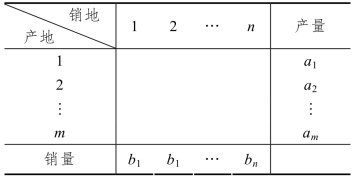
表3-2 单位运价表
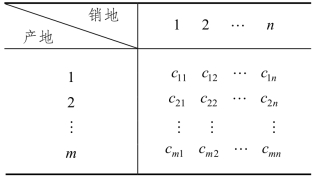
若用 xij表示从 Ai到Bj的运量，那么在产销平衡的条件下，要求得总运费成本最小的调运方案，可求解以下数学模型：
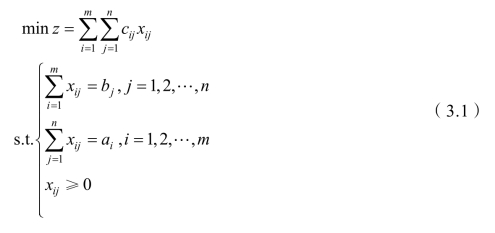(www.xing528.com)
这就是运输问题的数学模型。它包含（m×n）个变量，（m×n）个约束方程，其系数矩阵的结构比较松散，且特殊。
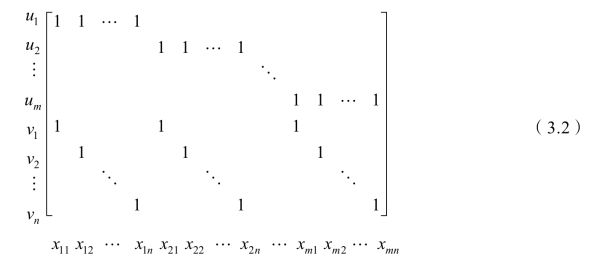
该系数矩阵中对应于变量 xij的系数向量 Pij，其分量中除第i 个和第m+j个为1 以外，其余的都为零。即
对于产销平衡的运输问题，由于有以下关系式存在：
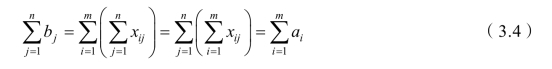
所以模型最多只有m+n-1个独立约束方程，即系数矩阵的秩≤m+n-1。由于有以上特征，所以求解运输问题时，可用比较简单的计算方法，习惯上称为表上作业法。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
