Par公司生产计划的Lingo优化分析及范围计算

上一章例1-12中，我们通过运用Lingo 求解Par 公司问题，展示了如何应用Lingo 求解线性规划问题。求解报告如图2-2 所示。正如我们之前讨论的那样，目标函数值是7668，最优解是S=540，D=252，对应于四个约束条件（第2～5 行）的松弛变量值分别为0，120，0 和18。现在，让我们考虑一下递减成本列和对偶值列的信息。

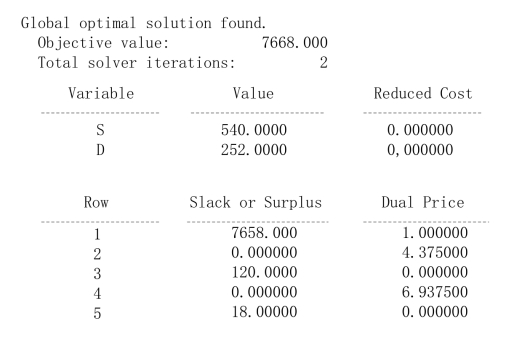
图2-2

关于Par 公司问题，两个决策变量的递减成本均为0，因为这两个决策变量都是正值，Lingo 给出了对偶价格（dual price）而非对偶值。对于最大化问题，对偶价格和对偶值是相同的；而对最小化问题，对偶价格等于对偶值的负值。关于这个独特的问题，是有其历史原因的，因为这超出了本书的范围，暂不做讨论。当理解最小化问题的Lingo 输出解时，只要将对偶价格乘以-1，然后将得到的结果作为对偶值即可。约束条件1（第2 行中的切割与印染约束）有一个非零的对偶价格4.374 957，约束条件3（第4 行中的成型约束）的对偶值是6.937 530 0，这告诉我们，切割与印染工作时间额外增加1 h，会改进（增加）最优解值4.37美元；成型工作时间额外增加r（h），会改进（增加）最优解值6.94 美元。

接下来，让我们考虑怎样用Lingo 计算每一个目标函数系数的最优范围以及每一个对偶值的可行域。在默认情况下，Lingo 不能进行范围计算。为了使得范围计算可行，需完成下面的步骤：

第一步：选择Lingo 菜单

第二步：选择Options(www.xing528.com)

第三步：当Lingo的选项对话框出现时：

为了使Lingo 执行范围计算可行，现在必须再重新求解Par 公司问题。重新求解该问题后，关闭或最小化求解报告窗口。为了显示范围信息，选择Lingo 菜单的Range 命令。Lingo在一个名为“Flange Report”的新窗口中显示范围信息。出现在Par 公司问题的范围报告窗口中的输出，如图2-3 所示。

图2-3

我们将利用范围报告中目标函数范围部分中的信息，来计算目标函数系数的最优范围。例如，S 当前的目标函数系数是10，注意到其相应的允许增加值是3.5，相应的允许减少值是 3.700 000，于是，S的目标函数系数CS的最优范围为：10-3.700 000=6.300 000 与10+3.5=13.5 之间。取整后，其最优范围是6.30≤CS≤13.50。同样，对于有允许增量值5.285 714和允许减量值2.333 300的CD，其最优范围是6.67≤CD≤14.29。

为了计算每个对偶值的可行域，我们运用范围报告中“Right-Hand-Side Ranges”部分中的信息。例如，切割与印染约束（第2 行）当前的右端值是630，允许增加的值是52.363 16，允许减少的值是134.400 00。因为这个约束的对偶值是4.374（如Lingo 求解报告中所示），我们能推出，每额外增加1 h，将引起目标函数增加4.37 美元。根据给出的范围信息，我们看到取整后，4.37 美元的对偶值在高至630+52.36=682.4，低至630-134.4=495.6的范围内是有效的。于是，切割与印染约束的可行域是495.6～682.4。其他约束的可行域可以以同样的方式确定。