技术系数的变化带来的生产收益增加

例2-8　分析在原计划中是否应该安排一种新产品，以第1章例1-1 为例。设该厂除了生产产品Ⅰ，Ⅱ外，还要生产一种新产品Ⅲ。已知生产产品Ⅲ，每件需消耗原材料A，B 分别为6 kg，3 kg，使用设备2 台时；每件可获利5 元。问该厂是否应生产该产品？生产多少？

解　该问题求解的步骤是：

（1）设生产产品Ⅲ为台，其技术系数向量然后计算最终表中对应的检验数

说明安排生产产品Ⅲ是有利的。

（2）计算产品Ⅲ在最终表中对应的列向量：

将（1），（2）中的计算结果填入最终计算表1-6，得表2-12（a）。

表2-12（a）

由于b 列的数字没有变化，原问题的解是可行解。但检验数行中还有正检验数，说明目标函数值还可以改善。

（3）将 x3′作为换入变量，x5作为换出变量，进行迭代，求出最优解。计算结果如表2-12（b）所示，这时得最优解：x1=1，x2=1.5，x3′=2。总的利润为16.5 元，比原计划增加了2.5 元。

表2-12（b）

例2-9　分析原计划生产产品的工艺结构发生变化，仍以第1章例1-1 为例。若原计划生产产品Ⅰ的工艺结构有了改进，这时有关它的技术系数向量变为，每件利润为4 元，试分析对原最优计划有什么影响？

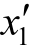解　把改进工艺结构的产品Ⅰ看作产品Ⅰ′，设为其产量，于是在原计算的最终表中以代替x1，计算对应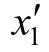的列向量。

将以上计算结果填入最终表 x1′的列向量位置，得表2-13。

表2-13

可见为换入变量，x1为换出变量，经过迭代得到表2-14。

表2-14(www.xing528.com)

表2-14 表明原问题和对偶问题的解都是可行解，所以表中的结果已是最优解。即应当生产产品Ⅰ′，3.2 单位；生产产品Ⅱ，0.8 单位，可获利15.2 元。

注意：若碰到原问题和对偶问题均为非可行解时，就需要引进人工变量重新求解。

例2-10　假设例2-9的产品Ⅰ′的技术系数向量变为=（4，5，2）T，而每件获利仍为4 元，试问该厂应如何安排最优生产方案？

解　方法与例2-9 相同，以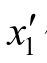代替x1，并计算列向量

将这些数字填入最终表2-14的x1列的位置，得到表2-15。

表2-15

将表2-15的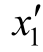变换为基变量，替换x1，得表2-16。

表2-16

由表2-16 可见原问题和对偶问题都是非可行解，于是引入人工变量x6。因在表2-16中x2所在行用方程表示为

引入人工变量x6后为

将x6作为基变量代替x2，填入表2-16，得到表2-17。

表2-17

这时可按单纯形法求解。x4为换入变量，x6为换出变量。经基变换运算后，得到表2-18的上表。在表2-18的上表中，确定x2为换入变量，x5为换出变量。经基变换运算后，得到表2-18的下表。此表的所有检验数都为非正，已得最优解。故最优生产方案为：生产产品Ⅰ′，0.667 单位；产品Ⅱ，2.667 单位，可得最大利润10.67 元。

表2-18