简便计算线性规划：对偶单纯形法

先从原规划的一个基本解出发，此基本解不一定可行（正则解），但它对应着一个对偶基可行解（检验数非正），所以也可以说是从一个对偶基可行解出发；然后检验原规划的正则解是否可行，即是否有负的分量，如果有小于零的分量，则进行迭代，求另一个正则解，此正则解对应着另一个对偶基可行解（检验数非正）。

如果得到的正则解的分量皆非负，则该正则解为最优解。也就是说，对偶单纯形法在迭代过程中始终保持对偶解的可行性（即检验数非正），使原规划的正则解由不可行逐步变为可行，当得到对偶规划与原规划的可行解时，便得到了原规划的最优解。

前面讲到原问题与对偶问题的解之间的对应关系时指出：在单纯形表中进行迭代时，在b 列中得到的是原问题的基可行解，而在检验数行得到的是对偶问题的基解。

通过逐步迭代，当在检验数行得到对偶问题的解也是基可行解时，根据性质（2）、（3）可知，已得到最优解。即原问题与对偶问题都是最优解。

根据对偶问题的对称性，可以这样考虑：若保持对偶问题的解是基可行解，即cj-CBB-1Pj≤0，而原问题在非可行解的基础上，通过逐步迭代达到基可行解，这样也得到了最优解。其优点是原问题的初始解不一定是基可行解，可从非基可行解开始迭代。

设原问题为

又设B 是一个基，不失一般性，令B=（P1，P2，…，Pm），它对应的变量为XB=（x1，x2，…，xm）。当非基变量都为零时，可以得到XB＝B-1b。若在B-1b中至少有一个负分量，设（B-1b）i＜0，并且在单纯形表的检验数行中的检验数都为非正，即对偶问题保持可行解，而且有：

（1）它的各分量对应基变量 x1，x2，…，xm的检验数是：

（2）它的各分量对应非基变量xm+1，…，xn的检验数是：

每次迭代是将基变量中的负分量xl取出，以替换非基变量中的xk，经基变换，所有检验数仍保持非正。从原问题来看，经过每次迭代，原问题由非可行解往可行解靠近。当原问题得到可行解时，便得到了最优解。

对偶单纯形法的计算步骤如下：

（1）根据线性规划问题，列出初始单纯形表。检查b 列的数字，若都为非负，检验数都为非正，则已得到最优解，停止计算；若检查b 列的数字时，至少还有一个负分量，检验数保持非正，那么进行以下计算。

（2）确定换出变量。按对应的基变量 xi来确定换出变量。

（3）确定换入变量。在单纯形表中检查xl所在行的各系数αlj（j＝1，2，…，n），若所有αlj≥0，则无可行解，停止计算；若存在αlj＜0（j＝1，2，…，n），计算按θ 规则所对应的列的非基变量xk确定换入变量，这样才能保持得到的对偶问题的解仍为可行解。

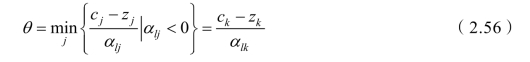
（4）以αlk为主元素，按原单纯形法在表中进行迭代运算，得到新的计算表。重复步骤 （1）～（4）。

例2-5　用对偶单纯形法求解。

解　先将此问题化成下列形式，以便得到对偶问题的初始可行基：

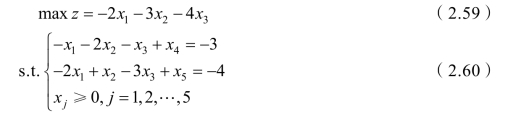(www.xing528.com)

例2-5的初始单纯形表如表2-4 所示：

表2-4

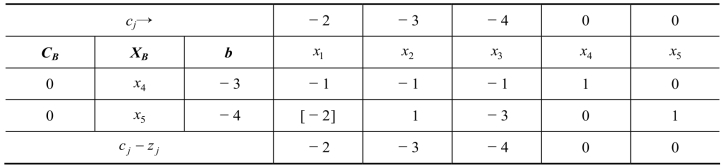
从表2-4中看到，检验数行对应的对偶问题的解是可行解。因b 列数字为负，故需进行迭代运算。

换出变量的确定：按上述对偶单纯形法计算步骤（2），即按对应的基变量xi来确定换出变量。计算：

故x5为换出变量。

换入变量的确定：按上述对偶单纯形法计算步骤（3），即在单纯形表中检查xl所在行的各系数 α1j（j＝1，2，…，n），若所有 α1j≥0，则无可行解，停止计算。

故x1为换入变量。换入、换出变量所在列和行的交叉处“-2”为主元素，按单纯形法计算步骤进行迭代，得表2-5。

表2-5

由表2-5 可以看出，对偶问题仍是可行解，而b 列中仍有负分量，故重复上述迭代步骤，得表2-6。

表2-6

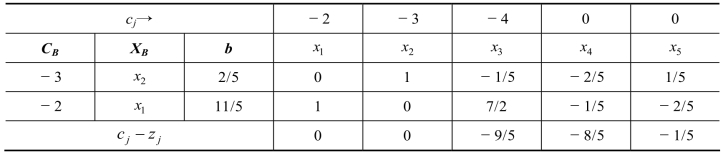
表2-6中，b 列数字全为非负，检验数全为非正，故该问题的最优解为

若对应两个约束条件的对偶变量分别为y1和y2，则对偶问题的最优解为

从以上求解过程可以看到对偶单纯形法有以下优点：

（1）初始解可以是非可行解，即当检验数都为负数时就可以进行基的变换，这时不需要加入人工变量，因此可以简化计算。

（2）当变量多于约束条件，即对这样的线性规划问题用对偶单纯形法计算可以减少计算工作量。因此，对变量较少，而约束条件很多的线性规划问题，可先将它变换成对偶问题，然后用对偶单纯形法求解。

（3）在灵敏度分析及求解整数规划的割平面法中，有时需要用对偶单纯形法，这样可使问题的处理得到简化。对偶单纯形法的局限性主要是：对大多数线性规划问题，很难找到一个初始可行基，因而这种方法在求解线性规划问题时很少单独应用。