对偶问题的基本性质与线性规划的证明

定理1　对称型对偶问题的对偶就是原问题。

证明　设原问题是

根据对偶问题的对称变换关系，可以找到它的对偶问题是

若将上式两边取负号，又因min（-ω）=max ω可得到

根据对称变换关系，可得上式的对偶问题：

这就是原问题。证毕。

定理2（弱对偶性） 若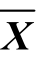是原问题的可行解，是对偶问题的可行解，则有

证明　设原问题是

推论1　若原问题和对偶问题都有可行解，则必都有最优解。

推论2　若原问题有可行解，但无有限最优解，则对偶问题无可行解。

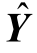定理 3（可行解是最优解时的性质） 设是原问题的可行解，是对偶问题的可行解，当时，是最优解。

证明　若根据定理 2 可知，对偶问题的所有可行解都满足因所以可见，是使目标函数取值最小的可行解，因而是最优解。

同样可证明：对于原问题的所有可行解满足

所以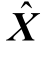是最优解。证毕。

定理4（主对偶定理） 若一对对偶问题（P）和（D）都有可行解，则它们都有最优解，且目标函数的最优值必相等。

证明 （1）设X*和Y*为原问题和对偶问题的一个可行解，有

（2）当X*为原问题的一个最优解，B 为相应的最优基，通过引入松弛变量Xs，将问题（P）转化为标准型：

所以Y*是对偶问题的可行解，对偶问题的目标函数值为(www.xing528.com)

X*是原问题的最优解，原问题的目标函数值为

证毕。

推论　若一对对偶问题中的任意一个有最优解，则另一个也有最优解，而且目标函数的最优值相等。

一对对偶问题的关系，有且仅有下列三种：

（1）两个都有最优解，且目标函数的最优值相等；

（2）两个都无可行解；

（3）若一个问题无界，则另一问题无可行解。

例2-2　已知线性规划问题：

试用对偶理论证明上述线性规划问题无最优解。

解　上述问题的对偶问题为

由第一约束条件可知，对偶问题无可行解；原问题虽然有可行解，但无最优解。

例2-3　已知线性规划问题

解　先写出它的对偶问题

它们为严格不等式，由互补松弛性得

因y1，y2≥0，故原问题的两个约束条件应取等式，故有

定理5　若X，Y 分别为一对对偶问题（P），（D）的可行解，则X，Y 为最优解的充要条件是同时成立。