标准型中系数矩阵有单位矩阵,很容易确定一组基可行解,这在前面已讨论了。但在实际问题中,有些模型并不含有单位矩阵,此时,为了得到一组基向量和初基可行解,需在约束条件的等式左端加入一组虚拟变量,进而得到一组基变量。这种人为添加的变量称为人工变量,构成的可行基称为人工基,可用大M 法或两阶段法求解。这种用人工变量作桥梁的求解方法称为人工变量法。下面介绍大M 法。
在一个线性规划问题的约束条件中加进人工变量后,要求人工变量对目标函数的取值不受影响,为此,假定人工变量在目标函数中的系数为(-M)(M 为任意大的正数),这样目标函数要实现最大化,必须把人工变量从基变量换出,否则目标函数不可能实现最大化。
例1-9 用大M 法解下列线性规划。

解 首先将数学模型化为标准型:
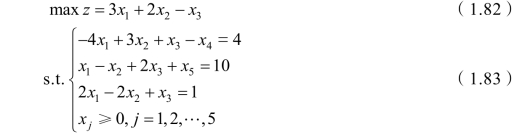
系数矩阵中不存在单位矩阵,无法建立初始单纯形表,故人为添加两个单位向量,得到人工变量单纯形法的数学模型:
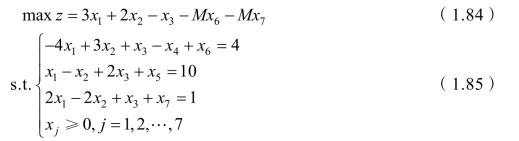
其中M 是一个很大的抽象的数,不需要给出具体的数值,可以理解为它能大于给定的任何一个确定数值。再用前面介绍的单纯形法求解该模型,计算结果如表1-7 所示。
表1-7(https://www.xing528.com)
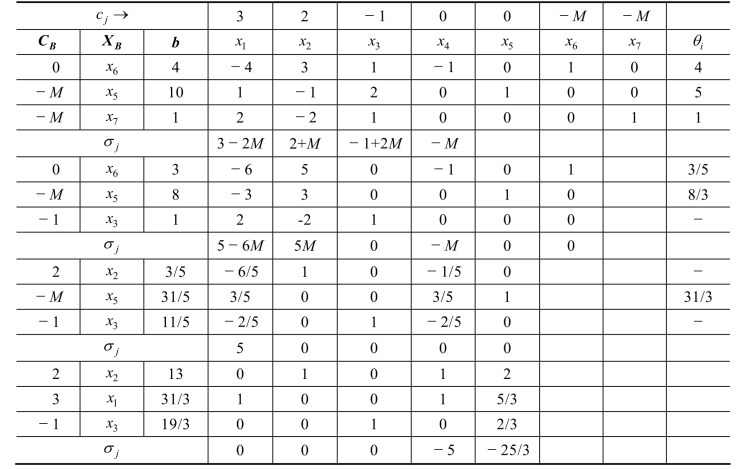
解的判别如下:
(1)唯一最优解判别:最优表中所有非基变量的检验数非零,则线性规划具有唯一最优解。
(2)多重最优解判别:最优表中存在非基变量的检验数为零,则线性规划具有多重最优解(或无穷多最优解)。
(3)无界解判别:某个λk>0 且aik≤0(i=1,2,…,m),则线性规划具有无界解。
(4)无可行解的判断:当用大M 单纯形法计算得到最优解并且存在Ri>0 时,表明原线性规划无可行解。
(5)退化解的判别:存在某个基变量为零的基本可行解。
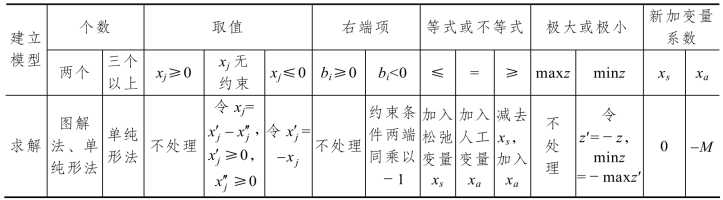
表1-8
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




