线性规划问题的定理和解法总结

定理1　若线性规划问题存在可行解，则该问题的可行域是凸集。

证明　为了证明满足线性规划问题的约束条件

的所有点（可行解）组成的集合是凸集，只要证明D中任意两点连线上的点必然在D 内即可。设

是D 内的任意两点，且X（1）≠X（2），则有

令X=（x1，x2，…，xn）T为X（1），X（2）连线上的任意一点，即

则X的每一个分量是将它代入约束条件，得到

又因，α＞0，1-α＞0，所以xj≥0，j=1，2，…，n 。由此可见X∈D，D 是凸集。证毕。

引理 1　线性规划问题的可行解X=（x1，x2，…，xn）T为基可行解的充要条件是X的正分量所对应的系数列向量是线性独立的。

证明 （1）必要性。由基可行解的定义可证。

（2）充分性。若向量 P1，P2，…，Pk线性独立，则必有k≤m。当k＝m 时，它们恰构成一个基，从而X=（x1，x2，…xk，0，…，0）为相应的基可行解；当k ＜ m 时，则一定可以从其余的列向量中取出m-k个与 P1，P2，…，Pk构成最大的线性独立向量组，其对应的解恰为X，所以根据定义它是基可行解。

定理2　线性规划问题的基可行解X 对应可行域（凸集）的顶点。

证明　不失一般性，假设基可行解X的前m 个分量为正，故

现在分两步来讨论，分别用反证法。

（1）若X 不是基可行解，则它一定不是可行域D的顶点。

根据引理1，若X 不是基可行解，则其正分量所对应的系数列向量 P1，P2，…，Pm线性相关，即存在一组不全为零的数 αi，i=1，2，…，m，使得(www.xing528.com)

即X（1），X（2）是可行解。这就证明了X 不是可行域D的顶点。

（2）若X 不是可行域D的顶点，则它一定不是基可行解。

因为X 不是可行域D的顶点，故在可行域D中可找到不同的两点：

设X 是基可行解，对应向量组 P1，…，Pm线性独立。当j＞m 时，有由于X（1），X（2）是可行域的两点，应满足

因X（1）≠X（2），所以上式系数（x（1）-x（2））不全为零，故向量组 P1，P2，…，Pm线性相关，与假设矛盾，即X 不是基可行解。

定理3　若问题存在最优解，一定存在一个基可行解是最优解（或在某个顶点取得）。

证明　设X（1），X（2），…，X（k）是可行域的顶点，若X（0）不是顶点，且目标函数在X（0）处达到最优 z*=CX（0）（标准型是 z*=maxz），所以它可以用D的顶点线性表示为

在所有的顶点中必然能找到某一个顶点X（m），使CX（m）是所有CX（i）中的最大者，并且将X（m）代替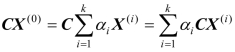中的所有X（i），这就得到

即目标函数在顶点X（m）处也达到最大值。

有时目标函数可能在多个顶点处达到最大值，这时在这些顶点的凸组合上也达到最大值，则这种线性规划问题有无限多个最优解。

假设是目标函数达到最大值的顶点，若是这些顶点的凸组合，即

于是

另外，若可行域为无界域，则可能无最优解，也可能有最优解，若有，也必定在某顶点上得到。根据以上讨论，可以得到以下结论：

线性规划问题的所有可行解构成的集合是凸集，也可能为无界域，它们有有限个顶点，线性规划问题的每个基可行解对应可行域的一个顶点；若线性规划问题有最优解，必在某顶点上得到。虽然顶点数目是有限的（它不大于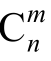个），若采用“枚举法”找出所有基可行解，然后一一比较，最终也可能找到最优解；但当n，m 较大时，这种办法是行不通的，因此，要继续讨论，怎样才能有效地找到最优解。找到最优解有多种方法，这里仅介绍单纯形法。