市场营销的定量预测方法及其应用

定量预测方法,是利用已经掌握的比较充分完整的历史信息资料,应用统计方法,寻求有关变量之间的规律和联系,建立数学模型,从而预计和推测市场未来发展变化趋势的预测方法。

在历史信息资料比较完整、准确,市场发展变化的环境和条件比较稳定,产品处于生命周期的成长期或成熟期,预测对象与某些相关因素之间呈现比较明显的制约关系,或预测对象随时间推移呈现比较明显的趋势等情况下,运用定量预测方法比较适宜。

常用的定量预测方法有:

1.平均发展速度法

发展速度是反映事物发展变化的动态经济指标,是报告期水平除以基期水平所得商数:

各个时期的发展速度是不同的,为了观察事物在一个较长时期中的平均发展或平均增减变化程度,就需要计算平均发展速度。计算平均发展速度一般采用几何平均法:

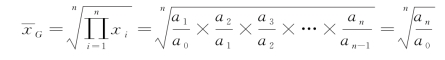
式中,n为项数,an为报告期水平(最末水平),a0为最初水平。

由此可见,平均发展速度的快慢,是由各环比发展速度的大小决定的,而且归根到底是由最初水平和最末水平之比,即总速度决定的。

[例4-1]根据某企业2008—2013年销售总额资料,计算平均发展速度(见表4-1):

表4-1　某企业2008—2013年销售总额资料

即,企业销售总额的年平均发展速度是135.24%。再进一步计算平均增长速度:

平均增长速度=平均发展速度-1(或100%),

即:

即,企业销售总额的年平均发展速度是135.24%,年平均增长速度为35.24%。

根据平均发展速度进行预测,公式为:

预测2014年企业销售额为:

即,2014年企业销售额预测值为1107.41万元。

2.移动平均法

移动平均法是根据原有时间数列,确定一定的时距,将每一项指标逐项移动,计算其动态平均数,形成一个新的数列,并用这个新数列来表现事物发展的总趋势。移动平均法考虑了动态数列发展的连续性,能把隐藏在原数列中的规律较为明显地反映出来。现以某企业甲产品销售额资料为例:

表4-2　某公司甲产品各月销售额移动平均数单位:万元

式中，为第t期的移动平均值,x为各期样本值,n为移动平均的项数。预测公式:

Yt+1为t+1期的预测值。一次移动平均法一般用于近期预测。

3.季节指数法

季节指数法是通过研究分析季节变动进行预测的一种方法。

季节变动是指某些现象由于受生产条件或自然条件因素的影响,在年度内随季节的更换而发生比较有规律的变动。如农业中的乳类、禽蛋等的产量,工业中以农产品为原料的轧花厂、禽蛋加工厂等的产量,服装市场中毛呢、汗衫等的销售量,交通运输中的客运量等,都是带有不同程度的季节变动的现象。

研究季节变动的主要目的,是预测未来季节变动的动向,以适应季节的波动节奏,合理组织生产,安排销售。

季节指数预测法首先需要根据若干年(至少3年以上)的资料,通过计算季节指数(也称季节比率),测定季节变动的规律性,然后根据季节指数和有关的年月预测值计算月(或季)的预测值。其具体步骤为:

(1)根据各年按月的资料计算出各月的平均数;(www.xing528.com)

(2)根据全部资料,计算出总的月平均数;

(3)将各月的平均数与总的月平均数进行对比,计算出各月的季节比率,即季节指数;

(4)根据季节指数和有关的年月预测值计算月(或季)的预测值。

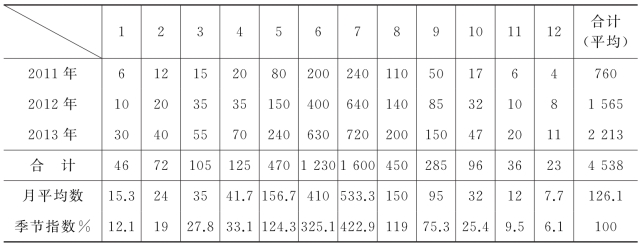
[例4-2]已知某厂生产的A种饮料2011—2013年各月的销售额资料如表4-3所示,当2014年预测销售额为3080万元时,计算其分月预测值。

首先根据月度数据编制季节指数计算表如下:

表4-3　A种饮料季节指数计算单位:万元

预测2014年1月份销售额:

2014年1月份预测销售额=

其余各月有关预测值的计算依此类推。

4.回归预测方法

回归分析是指对统计上具有相关关系的现象,根据其关系形态,选择一个合适的数学模型(回归方程),用来近似地表示变量之间的平均变化关系。采用的方法是配合直线或曲线,用这条直线或曲线来代表现象之间的一般数量关系。这条直线或曲线称为回归直线或曲线,它们的方程式叫直线回归方程或曲线回归方程。

回归分析实际就是将两个或两个以上变量间的变动关系加以模型化,其模型就是回归方程。如果是将两个变量之间的关系模型化,称单回归或一元回归;如果回归分析涉及三个及以上变量,称复回归或多元回归。经济现象中很多事物之间的关系形态呈直线关系,一元线性回归是回归分析的基础。这里主要介绍一元线性回归预测。

一元线性回归预测是指一个因变量与一个自变量有依存关系,在相关分析已确定了变量间存在着直线相关关系的基础上,配合线性回归方程来表达变量之间的平均变化关系。其表达式为:

Yc=a+bx

式中,x为自变量,Yc为因变量y的估计值,a是直线的截距,即当x=0时y的估计值,b为直线的斜率,即回归系数。a和b为确定回归直线模型的两个待定参数。

运用直线方程式进行回归分析,必须具备两个条件:

(1)现象之间确实存在显著相关关系(要通过相关分析进行判断);

(2)变量之间确实存在着直线相关关系(将两种变量的成对数值绘成散点图时,近似直线),才能配合简单回归直线模型。

作为最佳的回归直线方程,应满足两个条件:

根据最小平方法理论,用求偏导数的方法可推导求出a、b两个参数的标准方程组:

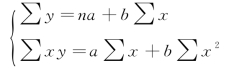
解联立方程得出:

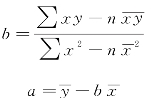
[例4-3]为研究某地区居民收入与文娱用品消费之间的关系,调查得到某地区人均月收入与年文娱用品消费数据,编制以下简单相关表,如表4-4所示。

表4-4　某地区人均月收入与年文娱用品消费的相关表

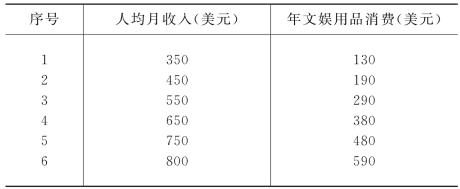
试建立人均月收入对年文娱用品消费的回归方程,并预测当人均月收入为900美元时,年文娱用品消费额。

表4-5列出了前述公式计算所需要的中间数值:

得:

回归预测方程为:Yc=-242.8219+0.990 7X

当人均月收入为900美元时,即X=900,代入预测模型:

Yc=-242.8219+0.990 7×900=648.81(美元)

即预测当人均月收入为900美元时,年文娱用品消费额将为648.81美元。