与科尔曼模型相关的值得思考的问题和完整循环

我们将尽量使用之前和本书第三篇之前的章节中用过的标记法。但当我们很快用完了这些常规标记法后，我们会重新定义一些术语并更广泛地使用向量矩阵标记法，这种标记法对于连接不同实体很有用。然而，该理论会用更传统的标记法来介绍，以便我们能将它直接联系到方程12.1到12.14中的最简形式的科尔曼模型。

假设决策制定结构包含I或L（I=L）个行动者、J个问题、K个因素和M个政策，并且给定行动者对问题的权力初始分布｛ri（1）｝。那么问题的重要性｛zj（1）｝可通过组合行动者权力和每个行动者对任一问题的利益程度｛Xij｝得出。那么

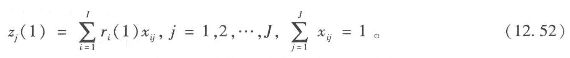
方程12.52究竟可预测什么是个值得考虑的问题。通过把任一行动者i的权力与该行动者对问题j表现出的利益程度相乘，可得出问题j对行动者i的相对重要性。然后，通过对所有行动者求和，问题j在整个体系中的总重要性就可算出。得出每个问题的重要性后，就有可能通过组合每个问题的重要性和每个因素与该问题的相关性来预测任一因素的价值。正式写作如此，

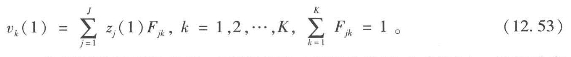
从问题的重要性出发，可得出第二组权力分布，即行动者用来决定政策意义的权力。通过组合重要性和每个行动者对任一问题被接受拥有的控制程度｛Cjℓ｝，可得出新的权力分布

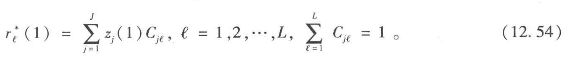(www.xing528.com)

此时，值得总结下已得出了什么。大体上，该理论通过组合行动者权力和对问题的利益得出了问题的重要性，然后通过组合重要性和对问题的控制得出了新的权力分布。第一次运算后，因素的价值也被预算出来，且这些运算包括解答出图12.1中箭头线f1、f2、f5表达的关系。

从新的权力分布出发，有可能经历两种相似的运算，包括预算政策的意义｛sm（1）｝。首先，组合权力和每个行动者对政策m的利益，由｛Wℓm｝的定义，可得出

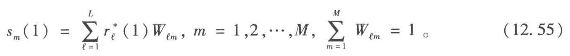
新的权力分布｛ ri（2）｝将被用来预测问题重要性的进一步分布，而现在｛ri（2）｝可通过组合政策意义和每个行动者对每个政策拥有的控制程度｛Gmi｝来得出。那么

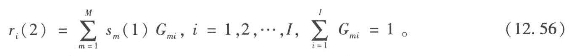
方程12.55和12.56代表了图12.1中f3和f4代表的运算，而且现在也很清楚地看到已经走完决策制定体系的一个完整的循环了。我们现在必须证明这个体系是否通过这个序列的连续运算达到均衡，如果是的话，我们需要讲清楚这个均衡的特质。在此之前，值得用矩阵形式再展示下这个模型，因为这样会简化接下来的分析。