选择最优设计机的霍华德算法实践：选强连接结构

也许这里提出的理论中最投机的部分在于设计机的设计。很容易看出，可以存在不同的机器，而有一些相比其他的更合适，但很难设计出相关标准进行选择。在这个特定背景下，一个最优机器是一定范围内可能替代结构的综合，这些结构的基础是反映因果或统计规律的不同关系组合。在设计领域中，一些争论集中于，因果关系或统计关系是否应该形成影响设计协调的基础，但是，因果和统计之间的区别只是设计机最优性的一种判断方法。好像有很多方法可以建立最优性，而评估这一最优性的原则很少，这一事实仅仅加强了这个观点的投机性质。正如我们在全书中尽力指出的，我们的科学是解释性的，而不是决定性的，对于城市问题和城市规划问题，需要包含多方利益相关者的多样方法。我们的科学目的在于展开讨论，而不是得到“答案”或“方案”本身，尽管我们以这些形式来表达观点。

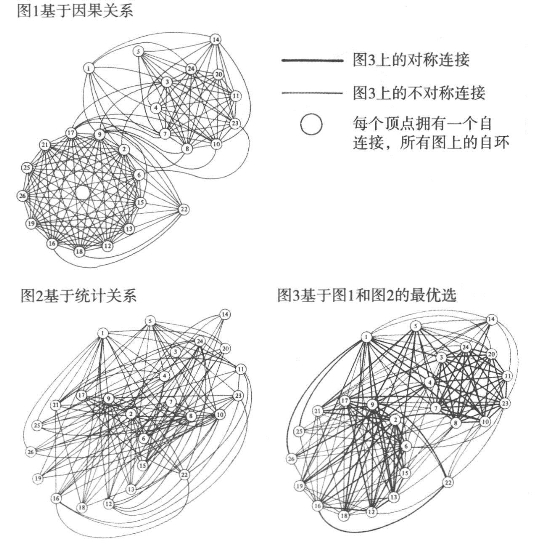
在图11.7中，展示了反映严格因果或统计关系的两幅图，以及直观选择的一些比较随意的回馈结构。第三幅图反映了使用上文提到的霍华德算法选择的最优结构。应用这个方法的一个问题是关于所选结构的连通性；显然，对于霍华德的方法或马尔科夫设计解决过程来说，最优机器必须是强连接的才有意义。在算法设计的过程中就已经对结构连通性进行了检查，不满足强连通性需求的结构被放弃，导致不太理想的结构被选中。有鉴于此，检查程序无法随意，而这又构成了一个有待研究的技术领域。

另一个困难是关于在原始机器中存在线性相关的可能性，或在寻找最优机器的过程中生成线性相关的可能性，特别是在处理基于二进制关系的设计机时。矩阵［pjkq］中的线性相关意味着，两个或以上的要素拥有相同的关系集，而这对设计机来说是不能辨别的。这对于更广泛的设计问题来说也有影响，而它的重要性取决于设计师评估关系集中的冗余度的方法。但从一个纯技术的角度来说，这可以是一个问题，特别是如果它出现在最优寻找过程中，因为它意味着关系增益不能被计算。实际上，在这个问题中，霍华德的算法从使用关系统计集开始，这个问题就不会出现，但如果这个过程从使用亚历山大-曼海姆的二进制矩阵开始，就会出现这个问题，因为这是线性相关的；这类相关性的影响可能会很重要。

(www.xing528.com)

图11.7　从两个可选系统中选择最优设计机

注：由于这类图非常难以绘制，通过构建第一幅图的理想形式，并根据这个形式绘制第二和第三幅图，以此来获得对不同结构的印象。

这个最优设计机的加权特性是通过方程11.25用传统代数来计算的，而最终解决方案见图11.8所示。这个解决方案与图11.5中展示的那些相似，而且也跟图11.4中展示的原始解决方案类似，从而说明了在生成设计问题的理性现实解决方案的过程中，技术是稳健的。