序时平均迭代结构及收敛特征分析

设计问题之复杂在于要为一系列相互竞争和冲突的要求（体现为要素）提出一个综合性解决方案，因此设计是一个协调和解决冲突的过程。此外，有观点认为设计不仅仅是简单的选择，而且是一个创造性过程，丘奇曼（1971）把这个过程定义为“为了弄清哪一个方案可以达到想要的目标或一系列目标，而概念性地从一系列可供选择的方案中做出选择的思考行为”（第5页）。这与任何一个方案都是可选方案或子方案之间的协调这一理念有共同的内核，这个理念也是上一章中问题构建的基础。在这个意义上，设计是在冲突的可选方案之间所做的选择。

我们将从重申上一章中介绍的平均方程开始，这些方程展示了包含问题不同解决方案的一系列要素是如何被互相协调的。实际上，在第10章中，我们将空间范围定义为一个要素，我们将在这里继续讨论，但如果将这个要素视为一个数值会比较简单，可以让我们更加具体地展示收敛到一个加权平均数的过程。在第10章中，我们定义了一个空间范围要素k——一幅地图，Ajk——这里我们将减少空间范围——由单元i赋值——简单的定义为要素Ak。从要素集Ak（t）=Ak开始，即时间周期t到t+1的初始状态，同时使用一个强连接的二进制连接矩阵［ajk］，新的平均值可以计算为

我们可以把网络标准化为一个跃迁矩阵，其中pjk=ajk/∑kajk。用这些定义，我们把这个平均方程11.1写为

然后，用Aj（t+1）替代Ak（t）来迭代方程11.2，我们得到

可以提取出一个总体的递归关系，在任意时间t+m的平均值为

我们在第10章中没做任何证明就提出，如果网络是强连接的，那么这个过程将会收敛。从第一个要素集中可以清楚地看出，任意子集之间的任意平均数会缩小它们的范围，而且如果一个要素可以直接或间接地影响任意其他要素，原始要素在最终解决方案中会变得越来越弱。如果这个过程继续下去，那么当m→∞时，极限，从而，设定开始时间为t=1，这个极限可以被写为(www.xing528.com)

其中c是最终要素解决方案的均衡态或稳态值，而［πjk］是稳态矩阵。

很值得用可视化方法展示这一方法实际上是如何生成加权平均的。图11.1a中，我们展示了一个假定网络，存在于五个设计师、行动者或要素之间——任何一个代表了读者想要放在问题中的对象——而后我们展示了一个强连接的有向图。在图11.1b中，我们展示了一个对称的二进制矩阵，而图11.1c展示的是基于其标准化的跃迁矩阵。注意这个矩阵反映了用于建立要素平均值的权重，不同的节点连接到这些要素上。在图11.1d中，我们展示了一个体现序时平均生成的前馈和反馈连接的迭代结构。在图11.1e中，我们展示了每个要素规定的初始值的收敛过程，其取值区间在3到10之间。这个过程从标在图11.1a中的节点旁的每个要素的值开始。这形成向量

而连续迭代得到

正如我们在下面会看到的，这个中值向量可以直接从网络的一些简单性质中生成。

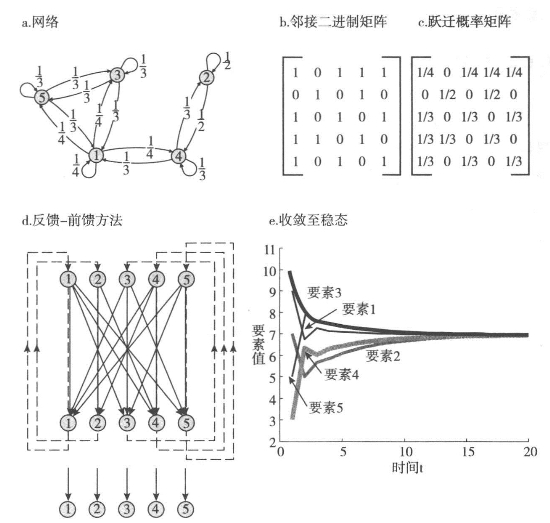
图11.1一个通信网络即意见收敛的说明性案例

值得一提的是，这一过程与一个被称为霍普菲德（Hopfield）网络的神经系统网络很相似（Gurney，1997）。在霍普菲德网络中，问题在于发现连接权重，以反映要素需要符合的特定值的目标集，简而言之就是提出输入要素的清单。神经网络包含了寻找网络连接的权重值，这些网络连接将这些要素转变为一系列已知的要素——比如一个模式。在这个角度来说，神经网络问题与设计问题十分不同，因为网络训练针对的是要素的已知模式，以确定输入要素怎样转变为这个模式。在设计过程中，不需要有这样的训练，而结束迭代的唯一标准是收敛到极限，在这里所讲述的案例中则表现为形成共识。虽然我们不会继续将它比喻为神经网络，但其中的很多建议颇具参考价值，例如将多元信息压缩为更收敛的形式，与这里建立的设计方法有一定的相似性，希望读者可以阅读这篇文章。