设计平均过程及其迭代结构

除了尝试通过建立网格状结构来减少信息丢失，还有另一种综合方法，这种方法中涉及问题的整个信息集都被使用。想象图10.4中展示的图是一个通信网络，其中顶点代表发射器或接收器，而边则代表频道。这张图可以被重绘为有向图，其中允许存在循环，而且两个方向上都有通道。图中的每个顶点上都有一个设计者，对设计问题的答案持有特定的观点；每个设计者都可以把他或她的观点发送给其他设计者，反之也可以接收其他人的观点，但只能通过给定的信道。这一权力结构的基础是对信息汇聚进行管理的清晰规则集，以及信息汇聚所带来的设计者观点变化。

通过将设计问题重新理解为解决不同要素或设计者观点之间的冲突，集体行动的目标就变成在遵循既定规则的情况下在所有成员间达成共识。假设每个设计者都可以完美地协调自己和别人的观点，那么解决冲突的过程按照如下方式展开。在第一个时间周期t中，每个设计者通过给定频道发送一个观点给其他设计者，同时，每个设计者通过对自己的观点和收到的观点做简单平均来改变自己的观点。然后，在下一个时间周期t+1中，这些新的观点按照相同的方式被发送并平均。这个过程持续直到每个设计者与组中其他设计者达成某种总体共识。这种收敛至一个与所有最初观点都不同的共识的情况，只会发生在基于强连接网络的权力结构中，因为只有在这种结构中，任意成员的观点可以传播给其他所有成员。妥协观点的连续传播逐渐减少了成员之间的意见差异，但最终共识是传播网络的体现，继而也是群体权力结构的体现。弗兰奇（French，1956）最早提出以这个模型为基础来研究社会权力，随后哈拉里（1959）对其进行了发展，并成为多种意见汇聚和学习方法的基础（Golub and Jackson，2010；Jackson，2011）。虽然在第3章中曾经介绍过，但我们这里仍然需要重温这种方法，以便将其与上文介绍的各种线性综合和层级综合方法进行比较。

图10.9　权力结构的有向图

需要注意，这个过程有一项重要特征是它代表了平均程序的一种简单类型。而且，按这种方法构想的设计问题引入了涉及真实程序的理念，包含权力和团体问题的解决以及连续决策。在图10.9中，无向图10.4被重画为有向图，图中沿着每条边的分数代表每个设计者相对其他设计者观点的直接权重。以这个公式为基础对设计问题进行综合并不算激进，问题中的每个要素代表了问题的一个部分解决方案。然而在应用之前，可以更正式地检验这个过程，以建立一个基于离散时间理论的代数表达——离散状态的马尔科夫过程。

考虑在任意时间段t+1中的平均或冲突解决的过程。这个过程包括要素Aik（t）的转换，在这里要素被记为与平均发生时间相关的形式，也就是起始要素Aik=Aik（1）。在时间周期t+1中，通过对所有设计者k到每个设计者j的连接的相关要素进行平均形成新的平均

实际上，我们可以用每个设计者给要素的权重来表达平均化过程。规定每个设计者给所有要素的权重之总和为1，条件概率定义如下

应用方程10.36，我们可以把包含方程10.35中序时平均数的递推关系写为

这里pjk是跃迁概率，矩阵［pjk］中每行总和为1，被称为随机矩阵，而一阶更新或平均化过程等价于一阶马尔科夫链（Kemeny、Mirkil、Snell and Thompson，1959）。

当然，方程10.35及其马尔科夫形式的方程10.36都是递推关系，任意阶段t+m的平均可以被认为是一个跃迁矩阵的函数，这个矩阵包含全部对原始要素进行平均的过程。接着，通过把Aij（t+1）替换为Aik（t）来对方程10.37进行迭代，我们得到

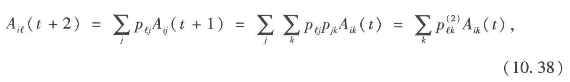
其中，具有较高的跃迁概率，可以推导出一般递归关系，从而任意时间t+m的平均值可以被表达为时间点t的要素值的函数(www.xing528.com)

如果网络是强连接的话，那么这个过程会趋于收敛。很明显，就原始要素而言，初始条件在最终答案中变得越来越弱，在信息发送中越来越包含信道强度。实际上，正如我们在第3章和第6章介绍的，可以看到，当m→∞时，，设定开始时间为t=1，方程10.39的极限可以被写为

其中ci是单元或用地区域i收敛到的平均值。

构成这类过程基础的正式理论是马尔科夫理论，而马尔科夫链被用于描述所谓的遍历过程，即能够从任意其他状态达到一个特定的状态。马尔科夫链具有额外的规律特性，因为对于某些指数的矩阵［pjk］，其所有要素均为正值。实际上，有一种对链进行完整分类的方法与等价马尔科夫有向图有关，但我们将到下一章再对链的分类和完整过程进行讨论，我们将再次正式介绍这个模型，并展示它在一个高速选址问题中的应用。

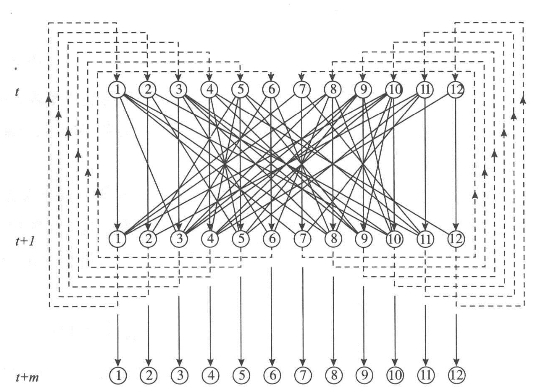
图10.10　作为序时平均的马尔科夫过程

作为总结，我们将使用方程10.39和10.40所表现的过程来说明如何进行平均。我们使用方程10.35或10.37具体说明迭代结构，其中每个要素Aik（t）在迭代时间t与其连接的要素进行平均，并在这个过程中生成Aik（t+1）。这个过程持续到收敛。在图10.10中，我们用图把这一过程展示为一系列反馈循环，有点类似神经网络中的反馈和前馈循环（Gumney，1997），而图10.11中，我们以图的形式展示了初始要素集12以及它们逐渐收敛到同一个值ck的过程。我们可以衡量每个要素在每个迭代时间t上的区别度，以测度收敛度，如

图10.11　限制图形式的空间平均

实际上，我们计算了跃迁概率，将其定义为

其中限制矩阵虽然不能通过直接的矩阵相乘来计算，但可以用马尔科夫链的其他特性来计算，我们将在下一章中探讨。这个收敛过程很快，我们将用较为简单的方法来说明。同样需要注意的是，与生成平均值相关的权重与这一收敛紧密相关，而且可以明确地计算它。这些，像大多数与本章中的强连接网络相关的权重一样，反映了网络的结构，而且为了完整性，我们在表10.2中列出了权重，以便可以用线性综合直接比较。实际上，正如读者会注意到的，这些权重与基本连接矩阵的入度和出度相同，在这个序时平均过程中，它的简单性深入地根植在这个表达问题结构的方法中，而其平均过程定义在这个方法之上，这个属性特别吸引人。读者将在下一章中看到为什么会这样，但这是处理强连接对称图的一个基本结果。