线性综合设计方案比较及优化

设计者对问题的看法决定了子方案或目标的集合以及限制条件，这些集合以及限制条件必须按照某种方式综合，来形成一个“最佳”方案。而且该方案必须与子方案有相同的形式，也就是土地适用值落在一个固定区间内，可以用图来表示。正如我们提到过的，这要求各个要素Aik当量相同，或在一定范围内具有可比性而不损失通用性，我们可以标准化为0≤Aik≤1，∀i，k。默认的综合方法是一个简单的平均，可以表示为

其中，我们假设要素可以被表示为限制条件或目标。如果要素是一个限制条件，我们可以用上标c来表示，而如果是一个目标的话，我们用上标o来表示。这与这些要素的取值一致

方程10.2适用于任意代表限制条件或目标的要素组合，因为它们在相同的取值范围内是相当的。

默认综合假设每个要素的重要性或权重相同。这可以方便地类推到不同的值，这样最终答案是一个加权平均值

其中的权重必须标准化，从而反映了每个要素的相对重要性。通常的形式中权重作为子方案或影响最终方案的要素的概率，那么就有

与前面的章节一样，在这里的案例中，如果范围很明显，我们将能够得出最终结果。

这个通过平均来生成解决方案的方法，被广泛地应用在选址有明确类别的各类实际土地使用规划中。有些时候，当要素表现为目标形式的时候，它指的是“发展潜力”，并且可以被作为等值面插入，如图10.2所示。这样定义的方法早在20世纪70年代在一系列子区域和大都市区的规划研究（见Wannop，1971）中就可以见到，这些方法现在是GIS技术坚实的组成部分。显函数可以让用户生成并视觉化综合解决方案，而这些理念如今已经被广泛应用于类似LUCIS（土地使用冲突识别策略）这样的实用方法中（Carr and Zwick，2007）

这些方法反映了地理设计领域的一些核心工具（Steinitz，2012），实际上，它们可以追溯到很早的景观规划研究，这类研究关注的核心是物理空间。显然，它们的极限在于，对于一系列相当的要素来说，它们必须包含用于开发的某种形式的物理适用性。简而言之，不管要考虑的问题是什么，它们必须被转换为空间形式，尽管这通常都是可行的，在表现特定要素时需要一些独创性。这些方法建立在我们称之为“叠加”的分析之上。可以图示的要素通过相互叠加来综合，要素假设具有相同的权重，并使综合平面成为一个不同要素的视觉组合或是受限制条件影响的区域的叠合。这一通常的过程是用于将要素表达为限制条件，并过滤掉那些不受任何限制条件影响的用地。斯坦尼茨、帕克和乔丹（Steinitz、Parker and Jordan，1976）描述了一段有用的历史，而霍普金斯（Hopkins，1977）介绍了一般性的连接叠加技术和更多正式方法。麦克哈格（McHarg，1969）的著作《设计结合自然》中提供了非常概括性的叠加方法，他将用于确定不同种类开发的最佳区位的方法描述为“叠筛图”（sieve mapping），这类开发中的要素表现为限制条件。基波（Keeble，1952）用以下方法定义这一过程：“它假设所有在检验的用地都“通过”一系列的筛子，每一个筛子代表了用于特定考虑目标的某种特有的渲染用地单元。任意土地使用特性由一个或多个筛子‘捕捉’来表达，当某块用地通过所有筛子，那么可以初步认定它适合考虑中的目标。”(www.xing528.com)

以限制条件作为过滤器或筛子来表达叠加图的一种方法，是通过叠合限制要素来形成的，即最终方案是

如果这是一个空集，那么说明每个用地单元k都被某种限制条件所影响，这种情况下就需要简单地对限制条件进行计数

当然，它与方程10.2中的非加权平均值相等。在图10.3中，我们通过综合图10.1和图10.2中的不同要素，展示了三个相关的解决方案，图10.1中的要素作为限制条件，而图10.2中的要素则是目标。这三个解决方案分别使用方程10.6中的限制条件、方程10.7中反映的叠加，以及图10.2中目标使用方程10.2的相同权重。我们没有采用不同的权重，在这个阶段或许比较武断。本章剩下的部分会探索我们如何基于要素之间不同的关联来确定这些权重。

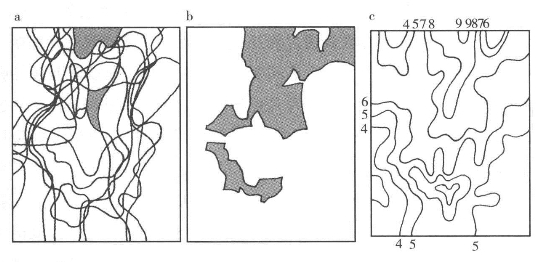
图10.3　不同线性综合的比较

注：a.传统叠加（筛选形式）分析，用灰色展示受到少于三个限制条件影响的土地；b.平均要素图，基于对限制条件的计数；c.相等权重的意愿平面。

在我们开始检验这类问题的结构之前，我们需要注意到不同的土地使用或活动可能会竞争土地，即当存在一系列我们提到过的设计问题时，在更高层面会有解决冲突的不同技术被设计出来。我们现在假设这些方法用于为一系列ℓ=1，2，…，L用地寻找最佳区位，其中我们结合前面的权重wk和要素Aik，用以设计符号表示的每种用地的最佳区位。在这个过程中加入这些不同用地之间竞争的一种方法，是确定每个解决方案的相对重要性λℓ，那么新的每种用地最终解决方案为

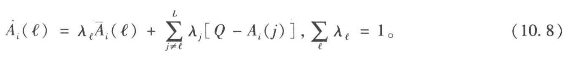
Q是合理定义的标准化因数，以保证决定每种用地方案的竞争面之间的可比性（Grant and Thompson，1971）。这个参数本质上将每种用地方案j≠k转换为与方案k的竞争。