设计问题的要素及其综合解决方法

设计问题倾向于定性而不是定量地表现它们的结构，因此基于统计或数值分析的经典研究设计并不合适。在解决任意政策问题中特别重要的是替代方案的定义，其中不同的方案与对象或限制有关，设计者根据手头的问题判断其重要度。阐明这类问题有很多方法，但在这里我们将考虑问题的任意解决方案与其他方案之间的联系。因此设计者的任务是把这些“部分”或子方案综合为一个令人满意的解决方案，其中影响最终方案的每个要素的重要性是清晰的。在这一原则指导下，不同解决方案的问题元素之间的关系将会通过一系列结构模型的定性关系来形成，这些结构模型构建在不同图论和网络表达之上，我们在本书的第二篇也应用过这些图论和网络表达。这些模型本质上是帮助思考规划的生成过程。就其本身而言，它们包含了可以作为承载规划问题解决方案理念的骨架结构。我们将要介绍的模型在很多年前就作为设计方法被建立起来，其中一些方法在实际设计和规划中仍然被普遍使用，特别在土地使用和景观分析领域，而另一些则是已有方法的衍生和重组。

在思考城市未来发展的时候，一个典型问题是如何使用土地以及如何组织活动，以满足特定的目标，这些目标是为了使区位变化和城市形态可以为城市生活创造更高效和更公平的条件。通常，大型居住区和交通如何选址属于这个领域的问题，但城市更新的很多问题也同样属于这个领域。我们在本章中将要讨论的问题是相对明确的，即寻找特定土地功能的“最佳”选址，以满足规划过程中所达成的特定预设目标。进行此类研究的最简单方法是在图纸上描绘出一定空间范围内的最佳区位和非最佳区位。因此一个问题的解决方案可以转换为一个空间数组Āi，其中有m个区位i，而且其数值可以是二进制的，当数值为1时为最佳区位，为0时为非最佳区位，但它也可以在一个范围内取值，比如从0到1之间，可以为某种特定土地使用的区位适合度赋值。

假设问题的任意解决方案为空间范围Aik，其中k=1，2，…，K个部分或子方案，那么设计问题的最佳方案可以被看作这些部分解决方案的联合体，即

每个部分解决方案都基于其对最佳方案的重要度，最佳方案反过来也会影响一些目标或限制条件。比如，对于现存零售设施的可达性或接近度最大化来说的最佳区位问题，Aik是其可能的一种解决方案，该问题无疑是与区位问题相关的，这涉及土地使用或零售设施服务产生的活动。另一方面可能基于某些限制，所有用于开发的土地必须符合潜在的防洪标准，在这种情况下，Aik可以定义那些满足这一标准的区域以及那些不满足的区域。因此，这些子方案将会体现为“全部或全无”的发展或连续的发展可能性。总之，接下来我们会将这些问题称为“要素影响发展”，反过来它们会体现反映需求和其他内容的单独目标或约束条件。

当然，定义最佳解决方案的关键是详细说明子方案或子目标的组合方法，解决方案都体现在方程10.1的通用关系里。一个直接的方法是把要素集分割到包含某种形式的收益-成本或意愿度的目标中，以及分到形成解决方案限制的约束条件中，然后按照优化的方式来解决这个问题。这往往很难完成，因为即使单一的约束条件也可能不可更改，当考虑到其他约束条件时，设计中会存在一定的可变性。比如，当位于平地或缓坡地带的大多数住宅开发是具有成本效益的，但有时候优秀的设计会打破这个限制，并在陡峭的地带进行开发。这在一定程度上反映了不可量化的要素，也反映了设计者的灵感和直觉。此外，设定了通过这样的优化程序来解决的问题，就假定了较难实现一定程度的量化。实际上，更为明显的一种方法是提供某种程序，按照可以控制实现的顺序考虑这些目标和限制，同时，随着解决方案的逐步发展，设计者在每个阶段仔细反复考虑。这是我们在这里将会关注的方法。简而言之，我们将为提供结构性的方法综合每个要素，推导出设计者可以逆向退回的解决方案，并可以在任意阶段改变综合过程。

为此，我们引入一个假想问题，为一个英国小镇的住宅开发选择合适的用地区位。这个例子以北柴郡的麦克尔斯菲尔德为原型，其现有市区人口大约为5万人，而更大区域范围内还有另外2万人，将位于可能选址的新开发空间中。我们确定K=12个关键目标，作为这个问题的关键要素，这些目标列在表10.1中。规划的任务是利用这些要素生成这个问题的解决方案。这个要素集几乎肯定是不完整的，所以这个问题在某种程度上是假想问题。尽管如此，它仍然是一个有意义的案例，可以展示本章中介绍的第一类主要设计方法。所有这些要素都可以用空间术语来表达，并且每一个要素在考虑的空间系统内都可能对不同的区位有不同的影响。我们在图10.1中展示了在严格限制下的12种情况，其中1（或黑色）说明了考虑中的区位不能开发，而0（或白色）说明该区位可以开发。在图10.2中，我们把这些作为空间意愿度来展示。其实，我们现在介绍的方法中，这些相互比较要素的顺序反映了每个要素在最后的“最佳”解决方案中的相对重要性。注意这个定义中的模糊性，因为假设了在任意阶段设计者的直觉都可以全面掌控这些顺序，它说明了我们生成的比较顺序只是推荐设计者遵循的一种。(www.xing528.com)

表10.1　影响居住开发的关键要素

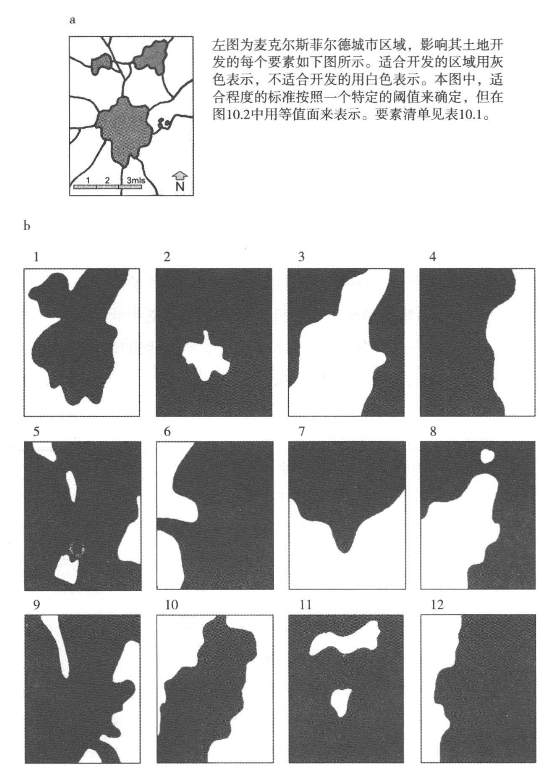
图10.1　要素表达为选址问题的部分答案

图10.2　要素表达为对最佳区位的渴望度

传统上，规划师根据这些要素对于解决手头问题的需求度或合适度（或相反的情况）将它们表达为空间形态，而规划生成和设计的过程是对这些要素的综合，它通过包括某种平均调和的方法来解决要素之间的冲突。我们接下来将要介绍的方法可能是发展最为完善的方法，最早由克里斯多夫·亚历山大（1964）详细提出，他认为每个与开发相关的要素，通常都包含一个非最佳的问题解决方案，比如表10.1中列出的那些要素。那么设计者的任务是检验每个子解决方案，并试图协调它们与每个其他子方案以发现最佳区位。12个要素可以有144（122）种可能的成对比较，但对于每个要素来说，生成某种与其他所有要素相关的综合解决方案，则将会有12种不同的方案。亚历山大（1964）认为，在对它们进行考虑的时候某种形式的优先顺序是有必要的，在这个基础上把部分解决方案或要素按照它们关联度或联系度分组，可以为生成12个要素之间最小冲突的综合方案提供一种好方法。这就是我们将在接下来的三个小节中说明的方法，最终将建立迭代法，可以通过这种方式综合子方案，形成一个真正的折中方案或“最佳”平均值。