城市能源消耗变化对出行决策的影响

图9.5　建立飞行场景：输入一条从希斯罗西部机场到CBD的伦敦西区的新重型铁路线

虽然这类模型实际上模拟的是均衡状态下的世界，但利用模型预测未来趋势会引起一系列动态矛盾，而这些矛盾会在新的均衡条件下得以解决。洛利（Lowry，1964）“速生大都市”初始想法的产生是基于这样一种概念，即校对后模型中的新生结构寓于已有均衡模式当中，只有通过模型对未来进行预测时新生结构才会显现。因此，校对后模型和未来状态之间的比较，就如同模型场景中发生新变化时把模拟的现状均衡（并非现实中的真实情况）和未来均衡相比较。而这些预测对于模拟相关变化的意义取决于模型的内部动态变化中蕴含的发展过程。

在地点和出行决策变化中存在着一系列不同的动态。对于出行决策来说，如果消费增加，那么人们很快就会转向低消费的出行网络模式。如果较为经济实惠的交通方式容量有限，那么交通方式选择的转换就会引起拥堵。这一过程需要时间来自行平衡解决，但是很可能要比位置变化的生效速度快。位置变化对于消费的影响显然需要更长的时间才能见效，居住地的迁移或许不会产生即刻影响，而职位分布变化（该因素不在本模型考虑范围内）也需要较长的变化周期。而实际影响因素往往是在那些位于第二或第三位的因素，它们需要较长时间的适应过程，而我们对这些因素知之甚少，因为它们往往与其他变化交织在一起。

我们可以对交通划分方式变化和位置变化做出严格区分，然而两种变化最终都会转化为基础设施分布变化，这种变化进程速度更慢。相比之下，用不同方式使用同样的基础设施，产生不同的活跃度则是一种快速变化（Wegener、Gnad and Vannahme，1986）。比方说，我们的模型最初设计时是为了测试气候长期变化带来的影响，尤其是未来100年内海平面上升对大伦敦地区人口分布的影响。在此期间，可能会出现重大变化或情况改善，因此未来的实际情况可能与模型预测的均衡模式有着很大区别。

实际上，均衡模型的重要之处在于它能够筛出必然会出现的变化。大多数同类城市仿真模型都是传统的“假如”（what-if）模式，这类模型一般用于提出并回答特定问题，例如“假如其他条件不变，当X改变时，它对目标系统产生了怎样的影响？”简单来说，模型能够体现明线和暗线影响中暴露出的因果链，在这一案例中就是指互动和区位两个因素。虽然模型能够确认互动和区位因素分别造成了多少变化，但是其中的平衡只能由整个模型的结构决定，而模型结构中包含了许多像这样的因果链。然而，基础设施变化则更加难以精准计量，因为在更长的时间范围内，基础设施变化显然还造成了相应的交通方式、线路、区位等方面的变化。而实际上我们所举的核心案例是有关消费变化而非基础设施变化的，从众多的可能性中选取一个来进行检验。我们要做的是检验公路交通消费翻一番后对其他交通方式造成的影响，也就是说，我们会整体提高系统内公路交通的消费，使单种交通方式消费翻一番，保持其他交通（即铁路、轻轨、地铁和公交车）方式消费不变。而适用于所有用户的其他交通方式不纳入分析范围之中，因为这些交通方式没有经过合理建模。汽车（k=1）的交通消费从状态（1）到状态（2）的变化可以写为：。如果我们把它代入交通模式对比方程9.10即可看出任何交通方式之间的交通量转化都是前一种交通方式的函数得出的，即

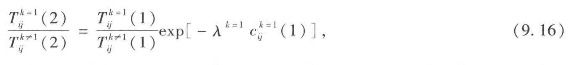
显然，高成本交通方式的消费增加越多，交通量的百分数变化就越明显。这一点符合逻辑，因为消费的增加可能会造成出行量的减少。

当我们按照这种方式把交通消费增加一倍以后，模型的预测结果在所有交通方式当中发生转变，正如行人寻找最实惠的交通线路，而且由于模型属性为单一限制型，居住地区位也会发生相应变化。这里有两个主要指标，其一是平均总交通消费，该指标在公路交通方面应当出现相应上涨（虽然交通方式变化很可能意味着公路交通消费并不会因外源性变化导致涨幅达到百分之百），其二是交通方式划分。相应数据记录在表9.1中，从该表中可以清晰看出平均交通消费总体上涨17%，其中涨幅最大的就是公路交通消费，达到27%。铁路和地铁消费仅上涨2%和3%，而公交车平均消费则略有下降，降幅为2%。这些变化几乎与交通方式划分结果完全相反，其中自驾出行下降了46%，相比之下公交车则上涨了42%。而铁路和地铁则分别上涨了35%和21%。如此显著的出行方式转换也会伴随着居住地区位的变化，这一点我们马上就会检验到。实际上，需要注意的是如此显著的出行方式转换并不会真正发生，因为实现这一结果需要修筑大量铁路基础设施并大幅扩展公交系统。然而，这就体现了系统中存在的压力，从这一角度来看，其结果与利用均衡模型探索未来具有一致性。

表9.1　平均交通消费与交通方式划分产生的变化

†实际平均交通消费和交通模式占比都是校对后的数据，因为模型需要经过校对才能满足这些限制条件。

原状态（1）和新状态（2）之间的交通量变化直接导致了方程9.4中终点住宅区活动的变化。从不同角度来看，这些变化可以由以下方式表达：

在该方程中，总交通量根据定义可以表示为：，设所有地点居住活动的差异总数为零，即：

简单来说，消费变化只会对已有活动进行重新分布，而模型预测的新均衡状态显然是一阶均衡模态，模型当中没有任何元素能够预测出其他各阶的效应，这种新均衡状态是由表9.1所示的区位变化和交通方式划分变化组成的。

我们可以生成两个更加生动的图表来表达这些区位变化，首先我们利用如下方程计算出总人口的绝对比例构成：

然后我们可以从任何一点将所有区域分为两个部分，Z1和Z2，因此两组区域的总和即可表示为Z=Z1∪Z2，(www.xing528.com)

方程9.20的用意是以任意方式将系统中的区域划分为任意两个部分，我们可以观察从一个子集到另一个子集所产生的流。这样我就可以比较出区位限制造成的影响是否在空间上偏向于系统中的某个区位，特别是在本案例中是否偏向于城市内部或郊区地带，从而反映出各地区在汽车使用方面的差异（Batty、Hall and Starkie，1974）。

模型得出的最令人震惊的预测是消费上涨后迁移居住地的人口数量Φ仅占总数的2.4%，约110736人次。这一数值非常低，反映了系统应对交通成本改变的弹性程度。然而如下图所示，虽然总消费会大幅上涨，但是实际上潜在的居住地变化造成的二次消费却比预想的要少很多。从某种角度上讲，这一结果只是解释了交互活动比区位有更高的变化自由度。图9.6展示了区位变迁的空间规律，从图中可以清晰看出，除相对比较活跃的西侧走廊能够吸引部分人群以外，其他地区城区人口相对集中而郊区人口相对减少。这一现象很可能是由于城市西部以及机场附近的就业岗位，以及与伦敦西部和西南部有良好交通连接的繁华的通勤者地带造成的。通过反复试验，我们得出了系统内的非连贯地区划分方式，使得大量人流穿过区界线。用户可以通过点击大范围或小范围（教区或自治市）来选择区划，从教区等级来看，有633种可能组合。显然，使用该工具需要对模型的工作方式和空间系统的结构有一定了解。

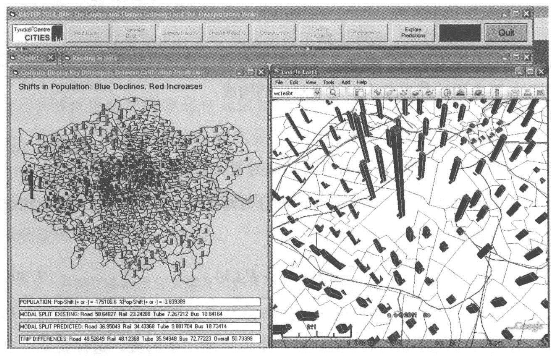
图9.6　公路交通消费翻倍对私家车造成的区位分布影响

注：灰色表示人口增长，黑色表示人口下降。

前文介绍的能源方程也为这些结果间接提供了参考。能源和熵的计量单位与模型输入数据单位完全不同，后者是按照形成所用时间以分钟为单位计算的。这是因为方程9.13和9.15中的熵是通过总交通量来计算，而不是像传统模型通过求导推出熵极大值中的概率来计算（Wilson，1970）。此外，方程9.13清楚地表明，不同交通方式产生的消费经过适当交通系数的计算，对结果进行叠加形成复合消费。然而，这些数值的相对比重在一定程度上解释了系统从第一状态（1）如何转化为场景状态（2）。我们把这些数值列在表9.2中，从中可以看出百分比的变化。

图9.7　基于非连贯地区划分的人口再分布

注：黑色表示人口减少，灰色表示人口增加。

关键在于，由于外部原因公路消费上涨100%，总能源消耗大幅上涨，致使自由能相应上涨，而熵只有轻微上涨，这意味着整个系统内交通的集中程度有所下降。总能源上涨幅度及其中自由能的涨幅很大程度上是由于公路消费上涨100%造成的，这种上涨极大程度上导致了交通方式的重新分配，而其他交通方式消费也因此出现了大幅上涨。显然，通过分解的方式我们不难看出，所有交通方式产生的消费的总和即为总消费。至今我们尚未对熵方程在不同交通方式下的分解进行探索。其原因在于，自由能方程中的耦合机理使得模型能够整体运作，因此自由能方程是不可分的，而这又会对熵方程的分解造成干扰。然而有关这一领域的研究方兴未艾，十分活跃。由于人们对于资源消耗殆尽和气候变化问题的日益关注，该领域研究也愈发得到重视。40年以来，熵极大模型中能源的真实含义始终处于沉寂的状态，直到现在才开始对这些概念进行量化计算（Batty，2010）。对于表9.2中的数据有很多种解析方式，读者可以参看威尔逊（2009）和莫费特（Morphet，2010）最近发表的几篇论文。有关城市的科学研究就应当指明能量如何在城市中进行空间移动，城市的状态（包括其物理形态和网络形态）如何对能源及其消费进行分布。基于这样的想法，本章希望提出一种前进的可能性。

表9.2　熵、能源和消费

为了进一步完善这一场景，我们将研究公路消费提高100%对于可达性的影响。图9.8对可达性变化进行了描述，我们根据对标准对数和也就是熵方程9.13中第一个因式进行计算，然后把它代入起点可达性中，也就是计算工作地的可达性。我们可以把每个重点的可达性变化方程表示如下：

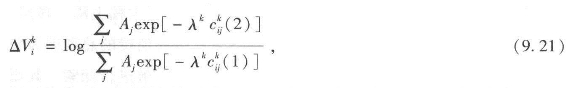
但是这种形式的可达性并没有在不同交通方式之间表达出明显的变化差异：在三种交通方式中，变化前（1）和变化后（2）的交通消费情况相同。然而，当我们对道路可达性变化进行检验时，从图9.8中，我们可以展现变化前、变化后的状态，并利用方程9.21计算出二者可达性的比率，设k=1。

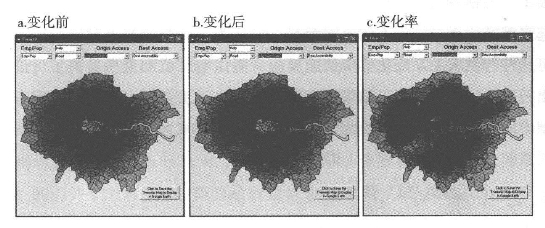
图9.8　道路可达性

二者的可达性状况在图中以等级的形式表示出来。可达性越强的颜色越深，反之颜色越浅。两种状态下的分布情况有一些相似之处——即可达性分布向中心地区聚拢——这一点在图9.8c二者间的比率中得到了更加清晰的表述。从图中可以看出，西南部的可达性有所降低，而中心收费区的可达性则有所增加，这是因为在交通消费普遍提高的情况下，消费更高的区域（伦敦中心市区）会变得更有竞争力，尽管其单位交通消费仍是该区域最高的。