基于单元模型的状态变化函数表达式及其应用程序

在开发空间应用程序时，我们可以通过多种方式来放宽元胞自动机模型的标准。首先，通过设定不同单元的发展速度，我们可以轻而易举地控制已开发单元的发展速度。如果发展速度是一个单位的单元，那么我们可以通过多种不同的外部限制来控制发展速度，但是正如所有放宽同质性规则标准的案例一样，这时的元胞自动机模型就不再能够以同样简单的方式生成图8.10中的突发模式了。而且，为了将多样性和异质性直接引入最简单的模型中，有时邻域中单元的单元计数或者串联会被转化成一个概率函数，这个函数继而通过一个随机数生成程序来调整发展速度。例如，方程8.6和8.7中的结构现在变为：

其中Pit为发展概率，而rand（Ψ）为随机数，比如说0到100间的任意一个数，这个数如果小于发展概率就意味着这块土地需要被开发。

我们可以通过这种方式做出很多调整，但最重要的调整是放宽严格的邻域规则并代之以某种超距作用。例如，将方程8.6中的Fit替换成可及性的引力表达公式，就可以得出：

由此可以得出一个能够预测相对可及性发展的模型：

这就几乎把元胞自动机模型转化成了一个可达性势能模型。这一模型是空间交互理论的核心，在20世纪50年代中期土地利用交通模型建立之初首次被提出（Hansen，1959）。我们在第2章中研究过这些模型，在下一章中我们还会继续探讨它们。当然，这里有一个问题，就是这样一个模型是怎样与应用广泛、历史较长的土地利用交通交互模型联系在一起的？这些模型在解释和预测能力上明显比我们这里讨论的元胞自动机模型更胜一筹，但是它们在动态处理方面的能力十分有限。我们很难把这两类模型结合起来，而且这也与我们这里提出的对城市的多元理解相冲突。

这些元胞模型的主要成就之一就在于根据不同土地利用类型确定了不同的单元状态，我们将这些状态区分开并标记为k，即为单元i在t时适宜的土地利用类型。在若干个模型中，这些土地利用类型相互联系，从某种程度上决定了一个地区被开发的区位潜力。我们可以将单元状态的变化表示为关于邻近单元土地利用类型的函数，并用函数表达式来说明一旦模型应用程序被投入使用，就必须明确状态变化类型。所以，t时单元i的新状态就可以表示为：

其中指完全统一定义的邻域且定义距离的区域仅限于所述地区。事实上，这从很大程度上放宽了严格意义上元胞自动机模型的标准，且这也是很多应用程序的特征（相关综述参见：Batty，2005以及Liu，2008）。值得一提的是，确定土地利用类型转变的规则一般会将领域的定义由严格的无超距作用原则转变为引力原则。这将不同的土地利用状态、密度和类型与不同用地联系在了一起，并将这些联系与不同的超距作用效应结合在一起。这些规则对于一个单元是否可以被开发，开发到何种程度等都有严格的限制，从而规范了不同用途的土地相互之间的联系。这些规则可以扩展到单元交通联系的发展。这些交通联系确保了不同用途的土地之间是相互联系的，并根据不同的生命周期效应来组织单元的再生。所有这些规则集在元胞自动机模型中都有所体现，而且它们对于SLEUTH、DUEM、METRONAMICA以及相关的模型包都很关键（Batty and Xie，2005；Batty，2012）。

更为普遍的元胞自动机结构是基于反应扩散结构的，这种结构与微分模型非常相近（微分模型在研究细微尺度上的物理现象动力学中应用非常普遍），可以表示如下：

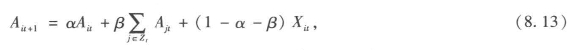(www.xing528.com)

其中α和β为0到1之间的归一化参数，Xit为外生变量，反映了那些可能被当作系统错误的外部环境变化，但是更普遍的情况是这些变化会被视为外部冲击，或者模型无法预测的一项输入。为了使这一结构更具可操作性，或许有必要加入其他限制条件来确保变量取值保持在一定范围内。

不过，这一结构本质上就是由反应、扩散和外部输入或者外部噪声组成的。如果我们假设Xit=0，那么系统演化或者生长就纯粹是一个关于系统反应和内部活动扩散之间平衡的函数了。事实上，这就是一个人造结构，因为所有绝对意义上的变化都需要加以控制。对于外部输入，情况总是如此。很多元胞自动机模型并没有采用这种更为普遍的模型，而且很多应用往往会提高已开发单元的输出来迎合外部预测，而不是如方程8.13中的反应扩散模型一样通过一种更为一致和微妙的方式来引入这种外生性。

针对元胞自动机模型的批评集中在对它们研究城市结构和形态变化高度物理主义的方式上。从本质上来说，这些模型都是供应方面的模型，以实体限制为基础来模拟土地的供应。需求的概念，以及交互作用的概念（体现在交通上）对这些模型来说是非常陌生的。我们在应用这些概念时，经常会涉及一致性原则，邻域限制原则和状态同质性原则，但是我们上述的模型并没有遵循这些原则，所以这些模型与土地利用-交通交互模型及其他我们在下一章中将介绍的模型之间还是存在一定差距。

然而，这些模型也有自己的优势，它们的优势就在于动态性。虽然在建模过程中，实际土地开发之外的动态进程并没有起到重要的作用，这些模型的动态性还是非常明显的。而且如果出现令人意外的预测结果的话，往往是由偶然因素导致的，因为这些模型模拟的一般都是相对平稳的动态过程。

图8.11　元胞自动机模型生成的常规扩散：类似文艺复兴时期理想化城市规划方案的模式

如果我们改变规则，要求一个未开发单元邻域里的单元个数必须为一个，那么我们就可以生成图8.1la中的扩散了，而且如果有一个或者两个单元，那么就可以模拟生成图8.11b了。实际上有上百万种可能，但是关键在于要确定一个正确的或者适宜的规则集。沃福兰姆（Wolfram，2002）在其著作《一种新科学》中说：自动机就是我们的宇宙赖之以建构的基本单元。虽然我们这里关于模型有许多要求，但是对这种自动机稍加调整，我们就可以复制许多不同的生成现象了，这些生成现象是许多城市形态的共同特征。

为了通过自动机生成理想的城市形态，我们有必要先建立一组现实的转换规则。理想的城市规划通常要满足一些主要的功能，例如最小化密度，如弗兰克·劳埃德·赖特的广亩城市；最大化密度，如勒·柯布西耶的光明城市；形成正式景观和花园广场，如摄政时期的伦敦；产生密度适中且根据不同土地利用类型进行分区的新型城镇，如第一代英国新城镇等。一个很好的例子就是通过元胞自动机原则生成的佐治亚州萨凡纳殖民地城市规划图。萨凡纳是由詹姆斯·奥格尔索普总督于1733年建立的（Wikipedia，2012），规划图如图8.12所示。我们可以类比图8.10和8.11来推导出图8.12的生成规则。

理想城市的规划通常都不是通过生成逻辑得出的，因为规划都需要整体构思，也就是说，关于一个不确定的未来，我们不可能有一个成形的概念理解。然而，通过元胞自动机，我们可以生成规划，并随时间演化，不断修改其规则以得出一个理想的版本。从某种意义上说，图8.10及图8.11中的规划是有恒定的规则的，它们可能会也可能不会被视为理想的目标。

为了总结我们对这一逻辑及城市内在复杂性（因为城市的理想形态永远不可能被确定下来）的阐述，我们将回到扩散限制聚集（DLA）模型，并对规则进行微调以实现我们的系统目标。想象一下，我们模型里的代理人是按照之前描述的方式随机移动的，也就是向八个方位移动；那么我们就可以假设代理人所在单元会根据代理人移动改变状态，并通过元胞自动机模型模拟这一过程。如果代理人原来处在单元（i，j），然后下一步移动到单元（i+1，j），那么代理人下一步所在单元的单元状态就会随之变为代理人原来所在单元的状态。我们的第一条规则，就是单元状态会由代理人原来所在单元转变为最新所在单元。但是我们也有一条这样的规则，就是：如果代理人处在单元（i，j），同时在单元（i，j）的邻域还有另一个代理人，那么代理人就不再移动，它所在的单元状态变为稳定状态。注意，在元胞自动机模型中，单元里的代理人包括移动的和固定（稳定状态）的代理人，或者一个单元也可能没有任何代理人。单元可能存在三种状态，三种状态都有编码，但是这仍然是一个有两个规则集的元胞自动机模型。我们可以建构很多类似的变体，来反映更为复杂的生长发展规则，但是我们的目的当然是选择在真实城市发展过程中切实存在的规则，同时又要让模型尽可能地简单。

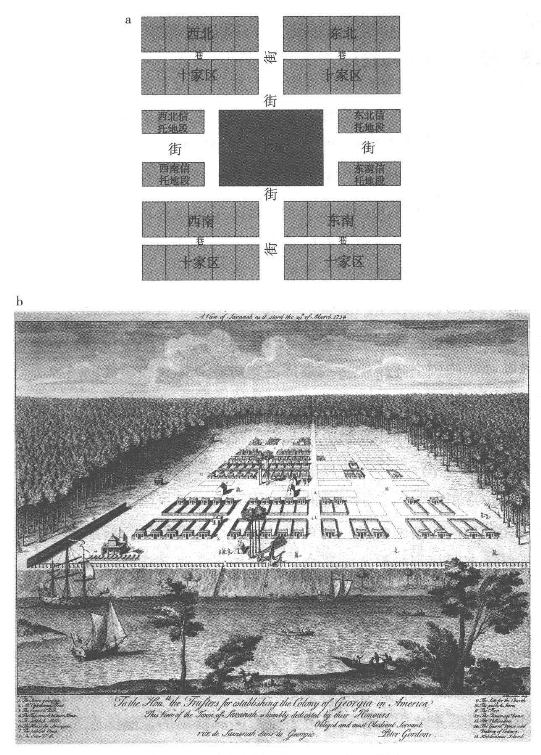
图8.12　佐治亚州萨凡纳殖民地规划

注：a.最早的规划，来自http：//en.wikipedia.org/wiki/Squares_of_Savannah，_Georgia；b.1734年的规划，来自http：//www.torontopubliclibrary.ca/content/ve/bain/images/111gordon-savannah-cons-large.jpg。