度方法的比较分析

空间句法和地理图之间的重大差别体现了两种类型问题中距离的本质和含义。在句法中，出发点是作为线的街道之间的拓扑关系，而在地理问题中的关系是对节点之间距离的物理测度。实际上，两种类型的问题是基于同样的街道系统的几何布局，但结果却令人困惑，这也使得空间句法自诞生以来就面临着意义和含义的争论。尽管我们已经在这里阐述了区别，空间句法并不是一种几何或物理距离，而只是关注空间中两个点和线之间是否存在关系。正如二部图中的邻接性（adjacency），原始或对偶拓扑图中的二部关系，或者从这些图中生成的步长距离，邻近度（proximity）是探究城市空间句法结构的核心分析工具。

然而还有其他邻近度的测度方法，看起来似乎都比传统的步长距离有重大优势。针对空间系统，贝拉和克拉拉蒙特（Beraand Claramunt，2002）构造了一个精妙的邻接性概念，考察一条线或一个点是否与其他线或点相连接，建立连接起点集与邻接终点集，然后对二者之间的共同点求加权总和。我们可以采用多种方法来表达直接邻接度，比如我们之前在方程7.5中用过的：当ℓik＞0时Zik=1，否则Zik=0。我们现在需要扩展这个定义以纳入对线和点的考虑，因此方程7.5变为：

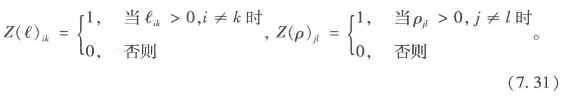
我们需要定义这些测度方法的出度（以及入度），因为这些决定了关联线和点的集合大小。从方程7.31可以得出：

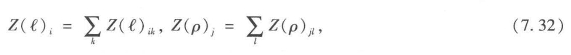
根据我们之前的研究，入度和出度在这里是对称的，Z（ℓ）ik=Z（ℓ）ki，i=k以及Z（ρ）jl=Z（ρ）lj，j=l。

新的测度方法可以将线（点的情况相同）定义为：

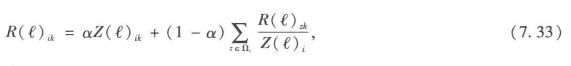
方程7.33右侧的两个部分都通过参数0≤α≤≤1取权重。第一部分是方程7.31所定义的邻近指数，如果一个元素i到一个邻近元素k之间有连接，则赋值为1。第二部分是一个相对测度，对起点集Ωi的邻近要素数量与关联k的终点集的邻近要素数量进行比较。这有些像一阶集聚系数，类似于瓦茨（Watts，1999）在小世界图中定义的集聚概念。加权总和本质上将i和k之间的直接连接与i和k通过元素z的有中间连接数量。如果i和k之间几乎没有共有连接，那么这个测度的影响将会降低，比如当权重都相等。当然，权重本身控制了直接和非直接邻近的强度。(www.xing528.com)

线性方程7.33的系统对于邻近矩阵（比如强连通性）的特定最小约束有唯一解。我们通过迭代对这个系统进行求解。由于这里的问题所涉及的规模较小，如加桑有41条线和63个点，墨尔本中心区有25条线和119个点，求解的过程很快，每个案例中的对偶或原始问题都不超过20次迭代。该解有一个重要特征，相对邻近度的结果矩阵［R（ℓ）ik］和［R（ρ）jl］并不对称，这揭示了一个事实，一个街道或交点集中从i到k与从k到i的可达性是不同的。然而其中没有涉及单向连接，因为本质上基本的邻近度图不包含方向。这意味着我们需要核查相关矩阵的出度和入度，对于线（以及随后的点）来说，它们可以表示为：

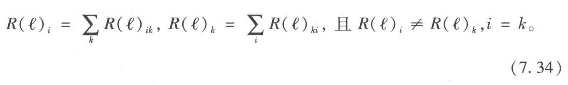
实际上，我们可能认为这些测度方法之间会很接近，因为方程中考虑的相邻集仅仅移动了一步。这要求我们提出能够度量超大步长情况下的高阶邻近度的方法。尽管贝拉和克拉拉蒙特（2002）没有在这个方向上继续拓展他们的方法，他们的研究展示了如何用多种变量对该种测度方法加权，这些变量反映了诸如距离、周边和区域等内容，并如我们在这里介绍的，提出了如何处理欧几里得距离信息。

我们以加桑和墨尔本中心区为案例介绍了这些邻近测度方法，并将它们与表7.1和7.2中的7种测度方法间的关联度，在表7.3a和7.3b中分别罗列出来。这里的比较呈现出与表7.1和7.2相同的结构，这两个案例中反映出在对偶和原始问题中，邻近测度方法与所有的传统测度方法有很强相关性，而与欧几里得测度方法则相关性很低。如同之前分析中与点分布的相关性，对于相对邻近度，两个案例中的出度指标的相关度都较低，因为点的出度几乎没有什么结构，反映出每个案例都接近平面性。相对邻近的入度和出度的相关度很高。对此，一种更加图形化的表现方法是用表面图来描述这两个案例，图7.12（a至d）描述的是加桑案例中的线和点，而图7.13（a至d）展示的是墨尔本中心区案例的线和点。

表7.3　加桑和墨尔本中心区的9种测度指标的相关度

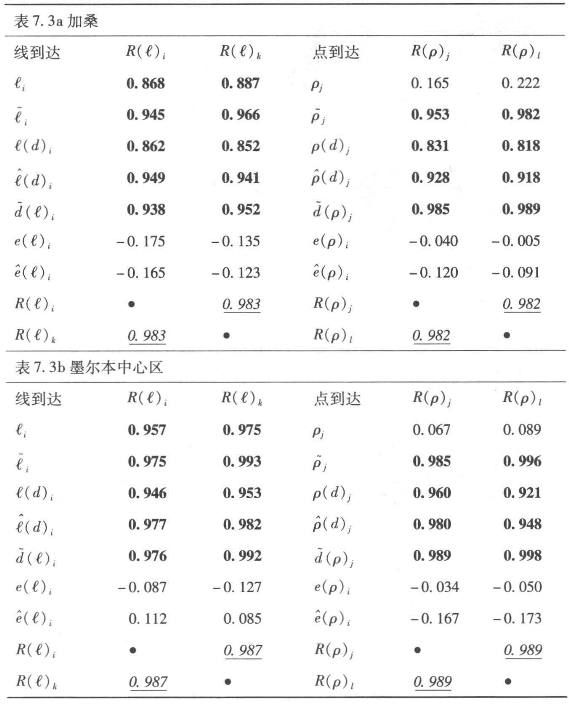
图7.12和7.13体现了在这两个案例中相对邻近测度方法是几乎对称的，这种情况应该存在于表面基本被街道覆盖的系统中。根据事物邻近（比如普查地块的管理单元）的真实结构进行应用，对称性的缺乏就更加重要，但是这些案例中并没有这种情况。实际上，邻近指标中体现了在加桑案例中，原始问题中线和对偶问题中节点的邻近度非常接近，除了北部轴线在原始问题中的重要性要强于对偶问题。墨尔本案例中，原始和对偶之间的一致性较低，基于线的原始问题表明邻近测度在中心区域的覆盖比起点在对偶问题中要大很多，其中南北轴线在可达性表面产生的条状带扰乱了覆盖。与欧几里得距离的测度不同，铁路站点的位置和由于它们远离视线而与街道系统相对不可达性，说明了在中心区域中这些点邻近度的相对缺乏。

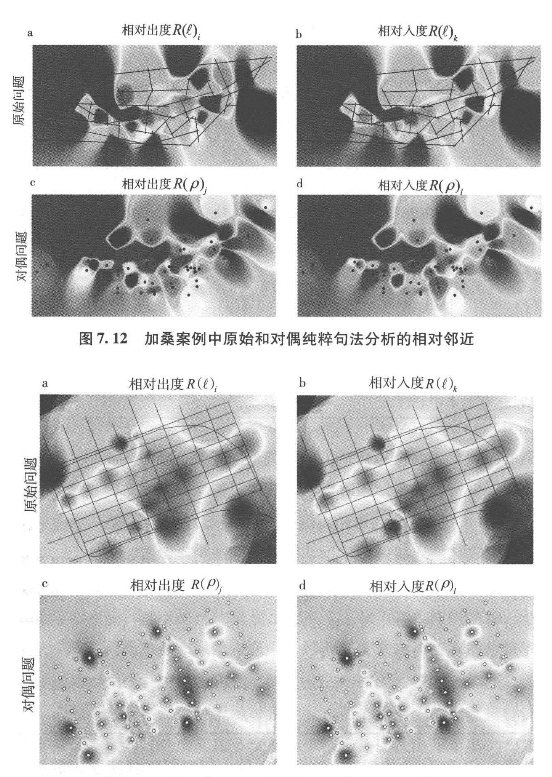
图7.13　墨尔本中心区原始和对偶分析的相对邻近