加权距离测度及其计算方法

目前为止，我们在本书中的假设是，我们所研究的空间网络是由直线——具有坐标的节点间的轴线或者直线段组成的，通过点的坐标我们可以计算直线的长度。实际上，通过近似精度处理将曲线视为由直线段组成，我们的研究对象可以很容易扩展到曲线，但是我们在这里将不会涉及（Figueiredo and Amorim，2005）。首先我们处理更加简单的对偶问题，对于一条线段的两个端点j和l的坐标分别为｛xj，yj｝和｛xl，yl｝。当j≠l时，对任何j和l间的直线i来说，其对偶问题的直接距离［ρjl］的值只能是1或者0。由于任意两点之间最多只有1条线，那么直接欧几里得距离djl为：

其中点的自距离djl显然为0。任意点j和l之间的最短距离可以通过标准的迪杰斯特拉（Dijkstra）算法来计算，在这里表现为如下的形式：

对方程7.18进行递归，直至图中所有的步长变为正数或者迭代次数s逼近图中点的数量m。

总体而言，矩阵［ρjl］与二维图的矩阵有所不同，我们用［pjl］来表示后者。一条线可以与多于两个节点相关，但这在二维图中不会发生，一般情况下［ρjl］的一些元素是正值且等于1。而矩阵［pjl］如图7.1a和7.1b所示，具有更加简化的结构。上一章中，我们将平面性偏差的测度从每条线上点数量的角度定义为Ψ（ℓ）=∑iℓi/2n，但是其他基于图上距离的测度可能是：

其中d（p）jl是对二维图和对偶句法图（可以很容易从［ρjl］得到）的距离测度。还可以从这些距离中得到空间相互作用理论中的行程长度。如果对每个连接都加载行程或移动量｛Tjl｝，那么系统的标准平均行程长度可以表示为：

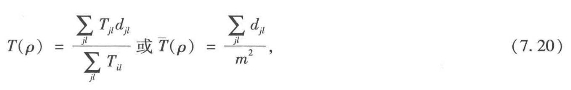
其中7.20的第二个方程体现的是当每个连接上的移动缺失或相等的情况，因此它们是统一的。

当然，通过行程长度可以计算每个点或节点，只需简单地将方程7.20与l而不是j叠加，或者与j而不是l叠加。但是更精确的测度是距离矩阵的出度的倒数形式：距离倒数的求和，以及每个点距离之和的倒数。这些是潜在的真实欧几里得距离：

以及

这些是对区位可达性的测度。根据第2章中讨论的传统社会物理学和空间相互作用理论，它们可以依据点的总量被加权，但是在这种情况下我们为避免混淆，并不打算对其进行加权。注意到方程7.22中的和的倒数，是与区位j的未加权平均行程长度的倒数成比例的。

对原始问题中的欧几里得距离测度更加棘手，因为我们需要计算每条轴线的重心。本质上，一条轴线可以与多于两个点相关，因此对这条线上的每条视线来说，都有一个重心点。例如在图7.1b中，轴线a'包含了3条视线，分别为1至2、2至3和1至3。因此对这些重心点简单地进行平均得出一个重心点是合理的，尽管可能需要再一次考虑变量的权重。我们首先计算轴线i上每条视线的重心点：

(www.xing528.com)

这些重心点需要进行平均，可以通过如下方程计算：

其中的求和包括了所研究的线上的每对点，并与所有相关点坐标的平均值相等。

如果一条轴线上对不同点的视图反映了不同程度的重要性，这个简单平均可以在不同权重的情况下增加，但在这里我们将沿用非加权的形式。我们现在可以通过计算从线i的重心点到连接了两条线的公共点j的距离，计算任意两条轴线i和k之间的距离。在轴线是直的前提下，这个距离是：

通过将非直线替换为细微的直线，并在方程7.25上进行递归计算，可以很容易地推广到非直线上。由于每条线有一个总长度，也就是有限长度，那么可以计算内线距离也就是自距，可以表示为：

在本书中我们认为dii=0，因为我们遵从空间句法的传统，但是也可以有其他的观点，由于移动性的影响认为自距是正值。

我们现在可以计算线之间的最短路径。我们采用方程7.18中计算点间距离完全一致的方式，即：

其中收敛性在时间s=n时得到保证。我们现在可以通过［dik］的倒数之和或者和的倒数的形式，来计算线的可达性，那么与方程7.21和7.22类似：

以及

我们在方程7.20中提到的所有其他涉及步长的测度方法都适用于此，如果需要的话，可以依据行程量对线进行加权。然而，正如在空间句法中，我们假设问题中并不一定需要涉及视线，而我们所需要的是一个对于线距的总体测度，也就是：