加桑数据：基准案例分析成果

我们已经介绍了加桑村的一些数据，这些数据表明与这些非欧几里得系统的关系集相比，轴线图是稀少的。图6.5就是轴线图，其入度和出度分别为［ℓi］和［ρj］，均为通过原始数据矩阵A计算得到的。全部潜在连接是指每条线都与每个点相连且反之亦然，而实际连接密度仅为5.1%。每条线上平均的点数量，也就是每条街道上的交叉口数量∑iℓi/n为3.385，而每个点上平均的线数量，也就是每个交叉口的街道数量∑jρj/m为2.129，这个值与平面性非常接近。我们之前注意到Ψ=1.065，意味着仅有略多于6%的点与等效二维图的配置不一样。实际上，在63个点中仅有6个点连接了超过2条线，而这6个点每个也仅连接了3条线。这是空间句法中一个令人担心的问题，所研究的系统缺乏多样性，会影响其他的可达性测度方法，如空间相互作用理论中的那些。更需要担心的是，空间句法中最为强调的线的关系是基于共有点的数量，如果大多数点只有两条线，那么线之间的拓扑距离的分布可能会处于一个非常小的区间里，由于实际上我们发现在很多应用中，图中的深度或距离很少会超过6或7个步长。这说明属于共有点和线数量距离的信息不应该被舍弃，因为这些信息在目前空间句法的距离计算及之后的整合中。

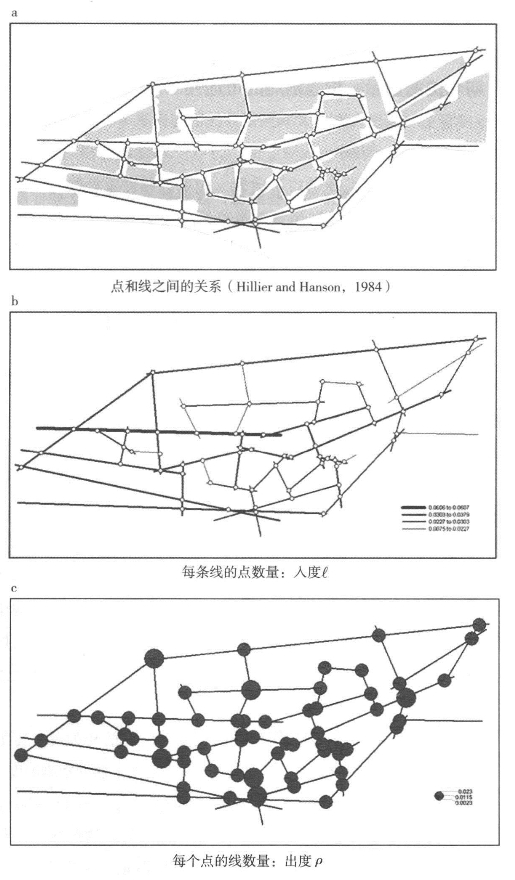
图6.5　加桑的基本数据：矩阵A所反映的点和线

我们首先检查原始和对偶问题的不同距离测度间的相似性，正如我们在之前对随机生成系统所做的。我们在表6.1中列出了四种距离测度，对原始问题是），而对偶问题则是，以及加权距离测度，这些相比其他任何测度方法对于可达性都有更好的识别力。表6.2（a）说明涉及线的原始问题的方法的相似性，而表6.2（b）是涉及点的对偶问题。对于线来说，基于原始数据的入度、基本距离和加权距离矩阵这一组的测度方法间具有强相似性，而在非加权距离测度ℓ（d）及其来自对偶问题ℓ"加权变体这一组间也是如此。这些测度方法组内的相似度在0.9左右，而组间的相似度约为0.7。对偶问题的测度相似性问题更为复杂，因为基本矩阵A的出度ρ几乎没有形成分布，而更像是阶梯函数。因此，直接距离测度和加权距离测度之间的相似性较少，而结果是在提取句法结构上，这些测度方法看来比其他任何与线结合的方法都要更有效。

表6.2　加桑的五种距离测度间的相似性(www.xing528.com)

为了更好展现这种结构和相似性，可以用散点图来展现入度ℓ与四个相关距离测度和ℓ，以及出度ρ与其相关测度、ρ（d）、和ρ"之间的关系。这些都标绘在图6.6中，从中可以清楚看到，线上的点数量缺乏多样性会使整个问题变得迷惑。这还需要进一步的研究，因为它的重要性会随着应用规模变大而增加。然而，这确实会涉及非常实际的问题。很多应用反映了图6.6中第二列的散点图特征，这其实是意料之外的规律。这表明这些应用的综合测度数量还跟不上移动量的增加，特别是对经常应用的行人交通对象而言。简而言之，很多此类应用中的统计相关性值得怀疑，原因很简单，就是基本数据的多样性不够。因此我们决定测度相似性而非相关性。

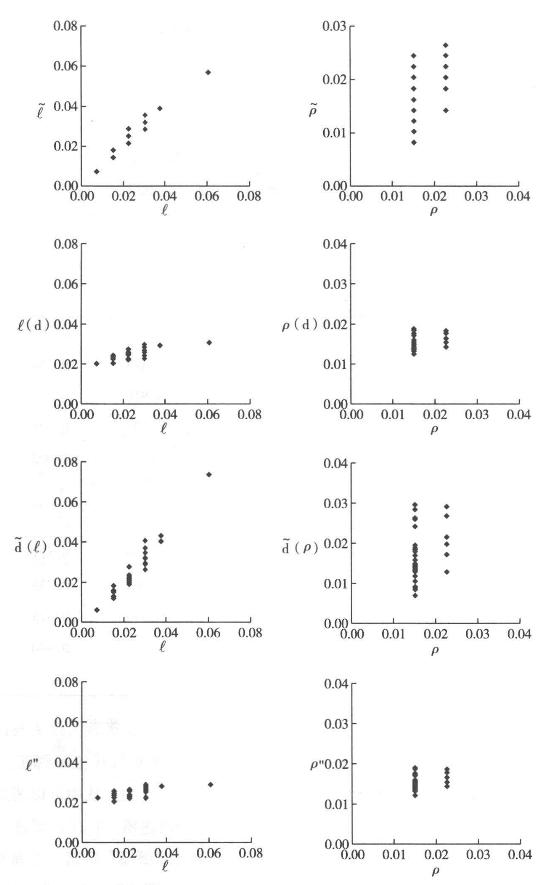
图6.6　从数据ℓ和P得到的连通测度相对于直接和间接距离测度的散点图