稳定态可达性的独特性：通过向量平均生成稳定态

展现稳定态的独特性的第二种方法，我们选择任意的距离向量，比如线的向量，然后通过连续的平均，生成越来越近似的稳定态。例如，从一个给定的向量，可以通过平均或依据，以此类推的序列给向量进行加权，得到一个更加接近的。对于这个关系，我们用任意迭代s的递归可以表示为：

由于Λ是一个马尔科夫矩阵（据定义是强连接），对方程6.36的递归会逼近于一个极限：

也就是方程6.34。对偶问题的类似过程是基于一个同样形式的递归，。实际上方程6.36提供了一个直接的方法来计算稳定态，而不需要同时求解从6.33到6.35的方程组。

然而，这里采用的定义中包含了一项不常见的简化，为了看清这点，我们提出初始数据实际上就隐含着稳定态。要说明这点，我们必须转换初始数据，以A来表达相关数据矩阵X和Y。然后，注意到ℓ=A1以及ρ=1A，用倒数矩阵［1/ℓi］和［1/ρj］中的nxnℓ（δ）维度和mxmρ（δ）维度形成对角矩阵，我们可以得到X=ℓ（δ）A以及YT=［Aρ（δ）］T=ρ（δ）AT。方程6.34中的稳定态关系就变为：

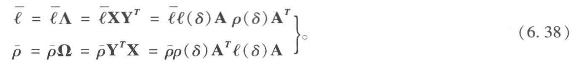(www.xing528.com)

让我们假设线的稳定态向量与线的原始数据向量是一样的，也就是是。那么，将其代入方程6.38，可以很容易得出：

对于其对偶来说是完全类似的，我们可以表示为：

简单来说，是一个相对令人惊讶的结果，这一稳定态实际上是由原始数据以及入度和出度构成的。这表明，对基于A的原始二部图简单进行入度和出度的计算，可以对线和点以及街道和它们的交点进行清楚和有意义的衡量。当然，这些衡量并不需要经过数字运算，而是可以通过对轴线图的分析简单读取。

然而，最令人感兴趣的是进行平均的过程。如果我们有对于线的距离测度，对于任何给定的距离测度，可以推导出平均点的估算为，ρ"=ℓ（d）X，以及。这不一定是恒定的，因为如果我们对这些平均点根据线的估算重新赋予权重，也就是得到ℓ'=ρ'YT，或者l"=ρ"YT，或者ℓ‴=ρ‴YT。这些可能与所用的原始距离有所不同，因为这些稳态关系的唯一向量是ℓ和ρ。此外，我们可以针对比如这样的情况，计算其与稳态的差别ρ'-ρ（对于其他所有的线或点的距离，都可以采用同样的方法）。这提供了一些指标，从中可以看到实际加权测度指标与稳态的偏离程度，而稳态是对系统中直接连通的测度。可以说，我们前面根据方程6.24计算距离差别时已经体现了这一点，具体可参见表6.1和图6.4 。