加权可达性计算：步长s与贡献关系

有很多种加权的方法，我们在此仅介绍其中一种。对于线与线间相互作用的矩阵［ℓik］，我们对每个矩阵幂s赋以权重ωs，并形成线性组合：

其中ωs随着路径长度s的增加而下降。如果我们将权重设为λs，其中的s是幂（同时也是个指标）且0＜λ＜1，那么当s→∞时，λs→0。线i的累积距离可以这样计算：

我们可以将总和的范围超过s而达到一个由规模λs决定的值。当s是矩阵规模时，所有的步长都确定为正值且λn＜＜1，但通常范围是固定为s且所有步长为正值的。对偶问题的相同测度可以定义为：

这个定义说明每条路径长度对于总体的距离都有贡献，并且可以通过确定λ的值来控制。在加桑的例子中，我们设置λ=0.05。如果我们针对原始（线）问题来计算每个步长s的贡献，我们可以得出以下关系：s=1，Φ=0.717；s=2，Φ=0.178；s=3，Φ=0.062；s=4，Φ=0.025；以及s=5，Φ=0.019，在加桑的轴线图中，两条街道间的最大路径长度（或深度）为5。

现在我们对这两个问题中的每一个都有四种对可达性的测度：两种是基于直接或邻近距离，另两种基于所有距离。原始问题的向量包括ℓ、、ℓ（d）和；而对偶问题包括ρ、、 ρ（d）和。空间句法图中的平均深度或步长较小，例如在加桑为3.239，我们的猜想是这些测度之间是高度相关的。为了检验这个猜想，我们生成了1 000个随机点线系统，其中线的数量为30至60条而点的数量为40至80个不等。对于用关系总数量与潜在数量的比值来衡量的线和点的关系密度Θ=［1-∑ijaij/（nm）］，我们设置其范围为0.75至0.99。加桑的例子中，线的数量为41，点的数量为63，比值Θ=0.948，所以这些随机系统与我们的真实案例具有很好的可比性。因为我们在这些随机生成中排除了所有的分离系统，其平均密度Θ=0.825，平均的线数量为45，而平均的点数量为59。生成的系统是比较高密度的轴线图，平均步长约为2.6。这些是对比较不同测度方法的第一次粗略尝试，还需要更多工作来支撑我们在此提出的假设性结论。我们对每对距离提出一个相似度指标，我们以ℓ和为例在方程6.24中定义为：(www.xing528.com)

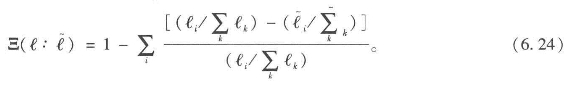
这个测度指标类似卡方，值分布从1（完全一致）到0（完全不同）。其他测度指标依照原始和对偶问题分别计算。

表6.1　四种距离测度的平均相似度Ξ

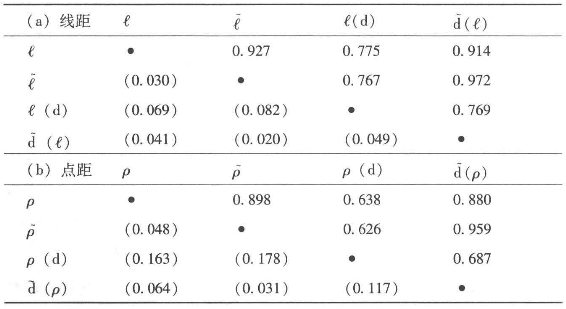
注：比较是对称的，位于对角线下方括号中数字是与角线上方相关相似度测度的标准差。

表6.1（a）和（b）比较了原始和对偶问题的距离测度。这些距离测度指标中的三个，分别基于原始数据矩阵A的入度和出度、基本相互作用矩阵L和P，以及加权距离矩阵，它们之间的相似度都超过80%。步长距离矩阵D（ℓ）与其他三个测度指标的相似度都在70%左右，而矩阵D（ρ）只有60%的相似度。这表明，当原始或对偶问题的轴线图中连接密度很高时，就像这里随机生成的1 000个系统那样，忽略了所有的非直接连接的可达性直接测度方法，是衡量线或点的重要性的好方法。正如我们下面将会看到，这些结果与下面给出的加桑案例中的结果非常相似，尽管图6.4中揭示了与d（ℓ），与d（ρ）之间的相似性还有很大的变化幅度。这表明当点的数量比线多时，正如在很多空间句法问题中那样，那么对可达性的判别主要依靠点。这或许看起来是反直觉的，因为空间句法更关注线而非点、更关注街道而非它们的交点。但是对于任何问题来说，如果其中某个集比其他集在数量上都大，那么这个集的重要性也会更高。我们将在后面对加桑案例的分析中重新提到这点，不过在这之前，我们还需要介绍关于距离的最后一个概念。

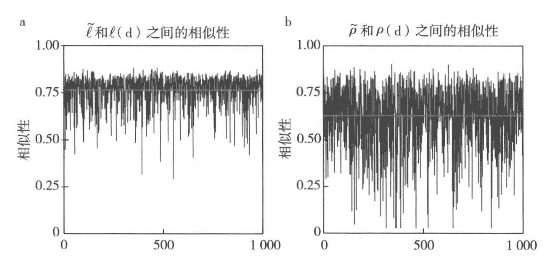
图6.4　直接距离和间接步距之间相似性的变化