城市网络的可达性及其表达方法

我们已经提出城市形态是一种诸如区位（点或区域）等可识别的城市要素所组成的格局。不同的区位之间往往通过城市街道等线性交通路线彼此联系。道路系统从某些方面来说就是城市发展的骨骼框架，因为它们为其他建设提供了重要基础。这些要素可以被认为组成了图的节点，节点间的关系弧代表了要素间的直接流或关联。这就是结构的概念，也是第2章和第3章所描述的各种相关工具和方法的基础。这些关系并不需要建筑实体这样的物理承载，因为在较为粗放的空间层面上这些关系可能是抽象的，例如区域之间的人口流动。然而，在较细致空间和更接近地方的层面，这些关系通常是线性的要素，比如街道或廊道等。此类分析的重点在于对节点间的隐形流进行建模，或者采用相对邻近法或到不同区位的“可达性”来分析隐形流。分析图中可能包括节点间的距离计算，以及不同区位及区位间连接所发生的活动密度和强度。例如，工作活动的集聚通常意味着较高的可达性。因此，规划和设计最多考虑的就是通过新建或更新交通基础设施改变可达性格局，以达到提升城市运行效率和空间资源合理配置的目的。

很长时间以来，一直有研究试图借助图论方法来表达城市形态。通过理想化的线路系统来描述城镇结构与交通的历史可以追溯到20世纪50年代末，比如斯密德（Smeed，1961）、霍尔罗伊德（Holroyd，1966）以及其他人（参见Haggett and Chorley，1969）的工作。在这之前，还有对区位组成的网络的研究和德国的区位理论研究（参见Isard，1956），更远还可以追溯到在第2章介绍的科尔（1841）。尼史顿和达西（Nystuen and Dacey，1961）提出了对区域中心地系统中的层级体系进行测度，康斯基（Kansky，1963）则将基本的图论应用于测量交通网络。基于围绕单点的加权合力，斯图尔特（Stewart，1947）提出了引力势概念并首先应用到人口系统分析中，其中就隐含着图的思想，我们在第2章中已经用它来描述流系统。之后的一些研究将可达性看作空间相互作用的决定性因素，其中也包含了空间系统的图论观（Hansen，1959；Wilson，1970）。类似地，图论还被广泛用于表现建筑中房间的连通性（March and Steadman，1971）和对建筑进行分类（Steadman，1983）。由于拓扑关系与欧几里得空间的紧密联系，长久以来图都被认为是用于表现其形态的基本结构。在对建筑层面或更大空间层面的增长系统建立生成模型和过程模型时，就如建立语法规则一样，建筑和更加集聚的空间对象间的关系具有相应的规则，这些规则促成了结构在其不断发展过程中的形成和转变（Stiny，2006；Lipp、Scherzer、Wonka and Wimmer，2011）。

在第2章和第3章中介绍的一般情形中，我们将欧几里得空间中的区位或点定义为节点或定点｛i，k｝，而它们之间的连接或弧为｛ℓik，i，k=1，2，…｝。连接的值可以是二进制的，表示存在或不存在，或是具体的物理距离dik。对于较小尺度上的系统，比如我们在这里所涉及的，通常关注邻里和建筑间的连通性，连接通常用二进制来表示：

在这种设定中，联系存在或不存在情况往往是对称的，即ℓik=ℓki；直接或间接的联系存在于任意两个节点间，就意味着潜在的图是强连接；而自关联ℓii通常被认为并不重要并将值设为零，即ℓii=0。我们将采纳以上这些假设，并且它们一点也不会削弱我们所提出论点的一般性。这种二元图中的可达性是依据它们的连通性来计算的，点或节点（入度和出度）间的直接连接可表示为ℓi=∑jℓij=ℓk=∑jℓjk，其中i=k。两点在图中的最短距离用dik来表示，这也可以用来衡量可达性。其权重需要取倒数成为与直接连接一样的可达性衡量指数，如，这也与直接连接一样具有对称性。这些衡量与第3章介绍的接近中心度等方法类似。

在较小层面的分析中，图通常是二维的或是被认为接近二维的，图中关系集的拓扑结构与欧几里得结构是相同的，即图就是街道或廊道的网络。其中假定任何弧的交汇都是节点且没有单向的连接弧（单行道）。图6.la是一张表达节点间可达性的图，我们将它作为原始问题。然而，还存在图6.lb中描述的另一种连接相关问题。如果我们寻找原始图中的连接弧之间的关系，对街道网络问题来说也就是找到每段街道间的关系，这就形成了被称为对偶问题的另一种图示方法。这里的对偶与更常见的所谓对偶的含义有所不同，后者是对原始二维图中连接所围合区域空间的关系网络的描述（March and Steadman，1971）。这里的对偶关系与原始连接并不一样，它们并没有与物理空间紧密相关，因为它们代表的是街道间的抽象关系。它们是通过街道在交叉点上的连接产生的联系，而原始问题则是交叉点间的联系，这种联系其实也就是街道本身。(www.xing528.com)

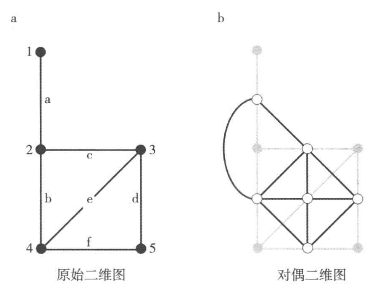
图6.1　常见的道路网络图论表达方法

对偶问题尚未广泛应用到城市的网络里，因为之前的关注是作为弧的通信链接，以及作为节点的特定区位交汇点。在前面的章节中，网络到目前为止仍然是在欧几里得空间内进行讨论的，网络被作为二维图或是节点位于二维空间中的图。相对于区位来说，对线性内容的关注并不多，对偶则主要将连线或街道作为关注对象，而非区位或街道交叉点。此外，对偶打破了欧几里得空间和拓扑空间之间的清晰联系，这使得对偶的可视化分析更加困难。不过，对偶分析中有一个运用广泛的传统工具即“空间句法”，最初由希利尔和汉森（Hillier and Hanson，1984）针对建筑内部空间的分析提出。其理论基础非常精细，认为可以将建造形态的进化类比为有机体生长的形态变化（Hillier、Leaman、Stansall and Bedford，1976）。空间句法如今的应用形式非常广泛，它更像是一个包括了很多简单技术的工具盒，可以衡量城镇街道的可达性，并与空间和视线间的无阻碍移动相关联（Hillier、Penn、Hanson、Grajewski and Xu，1993）。但是，与其他类似网络形态学方法相比（参见Sevtsuk，2010），空间句法的主要不同在于，它优先关注线性要素如街道，而非代表区位的点（Hillier，1996）。

图6.1描述了从原始问题转换为对偶问题的一条清晰路径，但这条路径并没有被很好地利用，至少在空间句法中没有涉及。本章中，我们将探索原始问题和对偶问题如何针对网络形态学代表了各自不同但又互补的角度，建立一个统一的框架使得任何人可以在这两类问题中随意转换。通过这种方式，我们将看到空间句法可以被转译为一个更加熟悉的区位分析框架。在下一部分，我们首先将对空间句法进行介绍，然后建立我们自己的框架，以更好地理解原始和对偶问题中的连通性和距离。接下来我们介绍希利尔和汉森（1984）针对法国村庄加桑的研究，以此为案例描述如何将空间平均运用于可达性计算。我们将展现如何将一个问题转换为它的对偶问题，以获得一种更好的可视化分析方法，并最终展示如何将距离重新带入空间句法中。同时，我们将描述如何通过这种扩展的形态体系来处理多类型的网络。

下一章完全建立在本章的基础之上，将通过一个针对伦敦西区数个街区的简单案例，介绍原始和对偶问题的所有研究结果，并且我们也认为这些方法可以被用于规划和非规划的不同道路系统类型中。我们还将进一步将距离纳入分析中，从而将分析带回道路系统，并提出通过这种扩展的形态体系来耦合不同网络的方法。在这两章中，我们希望将空间句法简单化并提出一个通用版本，为类似问题进一步的一般化处理指出方向，并讨论它们与网络进化和统计理论最近的发展之间的关系（Dorogovtsev and Mendes，2003）。