到目前为止,我们的等级模型都在关注城市等级体系的演化,而西蒙(1977)的定义似乎倾向于认为等级体系是固有的,已经存在的。为了确定等级结构,我们需要观察系统内部各部分间的相互联系并确定那些密切联系并构成整体的子系统。我们的模型需要明确这些内部联系,并将吉布列模型应用到网络结构中。通过随机增加单元和单元间联系,我们就可以做到这点。这个模型的运行机制体现在以下方程中。在每个时间段,对于一个与其他节点存在联系的已知节点,我们假设随机增加的联系量为δij(t+1)=1,其中Pij(t)指从节点i到节点j联系的总量。与i有关的所有联系量,总和即为i新的人口规模,表示为Pi(t+1)。故而,联系总量的方程可表示为:
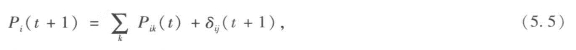
其中每个时间段更新的联系量为
![]()
是否增加一个联系取决于节点的规模及其与其他节点之间的距离,而这可以通过一个指数加权引力函数计算得出:
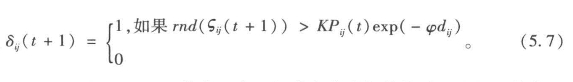
rnd(ςij(t+1))代表一个基于潜在交流规模的随机选择,其中dij指节点i到节点j的距离,而参数φ则表示这段距离中产生的摩擦效应。本质上,这个过程就是“优先连接”中的一种,因为在这个过程中,连接是根据现有连接规模及人口规模成比例增加的。巴拉巴希(2002)及其同事已经对这一模型进行了深入广泛的研究,并且发现这一模型会产生“无标度”网络,即入度和出度的数量是根据幂律成比例增长的(Barabasi and Albert,1999)。
另外,这一过程并没有考虑节点最初是如何产生的,因而,我们需要增加一个新节点产生的机制,类似于西蒙(1955)在他的位序-规模经典模型中增加的机制。如果随机变量rnd(v(t+1))大于预先设定的阈值z,则i处可增加一个新节点,表示为:(https://www.xing528.com)
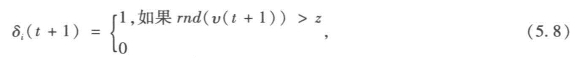
其中,z的取值小于增加新连接的可能性,如以上方程5.5到5.7所示。对于21×21网格,我们设置的新增节点阈值为z=0.1,意味着,在过程开始时每个时间段有十分之一的可能性会有新节点产生。当然,这一概率也会随着过程的推进而下降,因为如果选中新增的节点就是已经存在的节点,那么这一节点就作废了。关于已经存在的节点间连接的产生,首先根据与规模Pi(t)成比例的原则,随机选择一个节点i,而后根据方程5.7中的逆距离函数选择一个从节点i到节点j的连接,由此,整个网络结构就可以通过与现存节点“优先连接”的规则而建构起来。假设对于每个网格,系统总体尺寸为300 × 300(x-y坐标单位),那么方程5.7中的控制参数φ就可以设置为0.001,即为441个单元将近1 000个单位之间的平均距离。
图5.12中表示出了节点{Pi(1 000)}的最终人口分布,和节点间所有大于1的连接总量的分布,大于2的连接总量的分布以及大于4的连接总量的分布。这些分布图中存在着一个等级模式。我们可以在集群密度低于不同阈值的节点处切断连接,从而将空间分割为几个区域,来确定等级结构。我们并没有这么做,因为我们关注的不是等级本身,而是等级是如何产生的。在图5.13中,我们绘制了各个节点人口规模相对于位序的齐普夫位序-规模图。因为这个例子的数据量非常有限,所以图中的各点并没有连接起来,但是还是可以隐约看出图中各点呈现对数正态分布。将整条曲线看成一条直线,则其比例参数为1.05,变换率为90%。这与齐普夫定律分布图相当接近,在纯粹的齐普夫图中,参数γ=1。这也说明了,基于吉布列过程的“优先连接”模型确实可以产生同上述简化模型一样的分布。
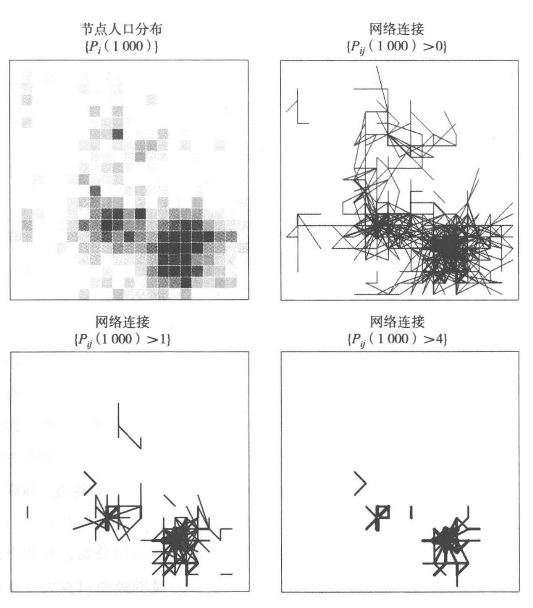
图5.12 网络连接模式
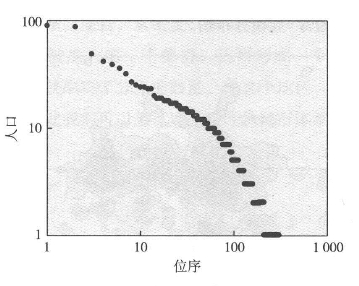
图5.13 节点网络位序规模分布
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




