竞争、交互和空间扩散下的城市等级体系模型及其消失机理

比例效应模型下的城市等级体系是所有可能存在的体系中最简单的。在这个体系中，对象的顺序由规模决定，并且对象之间都是相互独立的，因而这仅仅是一个简单单向的位序-规模等级体系。对于研究城市的发展来说，它也就不可能是个好模型，因为它并没有将任何形式的竞争或交流纳入考虑，所以在这个模型中，城市之间是毫无联系的。本章开头引言中西蒙（1977）所言与等级的定义相去甚远，因为在上述模型中对象之间并没有联系，但是仍旧产生了等级结构。我们现在所需要的就是城市或地区之间，网点之间某种程度的交流，不需要太多，来迎合西蒙（1977）的观点。为了将对象间交流纳入考虑，我们会在每个模拟阶段在相邻的网格单元之间加入简单的扩散活动。简而言之，在每个时间段，都有固定θ比例的人口会由单元i的各个方向迁徙到冯诺依曼区最近的单元k。因而，对于单元i而言，在t+1时人口Pi（t+1）可由以下式子计算得出：

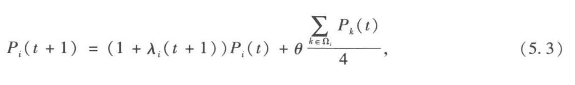
其中扩散区域表示为Ωi=knorth，ksouth，keast，kwest。这个模型考虑了最小限度内的远距离行为，而且在与一个网格维度成比例的时间间隔内，每个单元都会对除本身之外的其他所有单元产生影响。这种扩散作用还是很初级的，因为这个模型假定一定比例的人口会迁移到邻近地区，却没有说明这样的人口迁移行为具体出于什么原因，而只是笼统地概括为基于社会经济学原理。

我们根据方程5.3运算，并且在t=1 000，2 000，…，10 000这些时间区间里，保留了方程5.2中的截断部分，得出的位序-规模分布图即为图5.7。扩散程度参数设置为θ=0.3，意味着在每段时间间隔，每个单元有30%的人口迁移到了邻近单元。由此得出的分布并非比例分布，而是对数正态分布，正如之前不考虑扩散作用的模型一样。在这个模型中，截断部分事实上是被扩散作用抵消了，这与之前曼鲁比亚和安妮特（Manrubia and Zanette，1998）提出的模型相比略有不同。曼鲁比亚和安妮特模型与这个模型基于同一过程，但是没有设置阈值，而且只考虑正增长，因而得出的分布是符合比例定律的。但是，从某种意义上说，这些模型产生的分布是幂律分布还是对数正态分布都不重要，因为从现象学角度来看，所有倍增过程都隶属于同一类模型（Sornette and Cont，1997）。

图5.7

在这个模型中，所有的单元在每个时间段都会受到扩散作用的影响。这种影响不仅强烈而且持久，因为时间段的数量远远大于这个系统的规模（即21×21网格），以至于我们无法记录这些单元两两之间存在的交流。通过邻近单元的中介作用，远距离行为得以产生，也因此使得扩散路径组合的总量变得难以估量。人口最多的单元周围扩散路径最密集，正如城市中心往往人口流动最多。通过将单元与更高位序的中心（位序高低由人口规模决定）联系起来，并由此判断它们之间是否仅仅由于距离相近而联系在一起，我们绘制了一个简单的等级结构图，并对等级体系有了一个初步了解。图5.8为模型在t=100、t=1000及t=10 000时的增长模式，很明显，在一个地区100个时间段内产生的模式，随着时间的推移，也会在其他地点重复出现。通过确定最高位序单元，位序在其之后的3个单元，以及再之后的8个单元、24个单元，乃至最终围绕这一核心的64个单元，我们还可以得出以上图像的简化版。这能使我们直观地了解了人口密度的分布，也即等级位序的分布。

在图5.8中，我们展示了t=10 000时的模式，而且我们将每个层次的每个单元与位序更高的单元联系起来，不论单元之间存在直接联系还是仅仅通过相似值单元产生联系。由此产生的等级体系表示为图5.9中的半网格结构，类似于第1章中图1.lc的结构。我们不可能将每个单元与更高等级层次上的一个单元单独联系起来因为单元之间的联系无法切断，因而也就无法划定独立的区域。等级体系的这一表现是非常现实的。正如亚历山大（1965）在《城市并非树形》中提到的“交互影响”的概念，城市等级体系内部的联系也是交互错综的。经历了扩散过程后，等级体系中形成了一定的结构，但是模型还是同经历纯粹的吉布列过程后一样具有很大的波动性。在10 000年模拟期限中，所有441个不同的单元（即城市）都曾在某个时间段成为位序最高的单元，而且这些高位序单元的发展模式都显得毫无章法可循。

图5.8　空间扩散模式

(www.xing528.com)

图5.9　t=10000时的模式等级体系

由图5.10可以很明显地看到在模拟过程中，没有任何一个特定的聚落或者单个单元能够成为地区中心，长久保持在最高位序上。很明显，这个系统缺乏足够的延续性，因而并不能反映城市系统的真实情况，因为在现实生活中，在同模拟时间一样长的时间期限里，不可能所有的单元都能够成为位序最高的城市。因而我们需要建构其他模型。

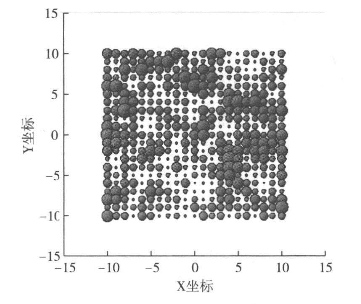
图5.10　10000年模拟实验中的高位序单元

注：气泡大小范围为1～83个时间段，其中相应单元主导的为平均23个时间段。

图5.11　当t=1000和t=10000时集聚模型产生的城市规模分布

经历吉布列过程和扩散过程产生的分布较为平直，而且随着扩散作用的增强，等级结构逐渐消失。通过减少吉布列过程的影响并引入聚集经济效应，我们希望能够增强模型的结构性。这样，我们的模型就变成了：

其中Φ和η反映了聚集经济带来的比例效应。假设Φ=0.2，η=1.08。通过这些参数，我们确实成功地优化了城市规模分布，但是如图5.11所示，这一模型依然保持对数正态分布，所以这一模型并不能带来任何实质性的变化。为了将不同形式的等级结构引入城市体系，我们需要从迅速发展的网络科学中汲取成果，来加深对城市间交互作用的了解（Barabasi，2002；Watts，2002）。接下来，我们将一一做介绍。