分析城市等级波动和分布规律性

幂律分布及其他类似的分布广泛地存在于城市以及很多其他分布中，例如收入分配。一百多年来，这已经成为一个不争的经验事实。19世纪末关于城市的理论，比如韦伯（Weber，1899）和奥尔巴赫（Auerbach，1913）的理论，已经把这看成是城市化的必然结果，当然，还有帕累托（Pareto，1896/1967）也提出了著名的收入法则，但是这一法则是基于频率而非位序的。我们在前面几章已经注意到，符合幂律比例分布的最佳例子就是齐普夫（1949）在其著作中所提供的那些例子，包括词频和城市规模分布。齐普夫指出，这些分布不仅仅存在比例关系，符合幂律，而且很多这样的分布（事实上是所有这样的分布）都符合逆幂律，这意味着不论是一个大洲、一个国家还是一个小镇，不论其规模和水平，人口位序都符合Pi（t）∝ri（t）-1=1/ri（t）。这就是齐普夫定律的强形式，它意味着城市规模分布是分形的，因为不论城市规模大小，分布都是一样的。这就是一种自相似性，而且这意味着分布是重新调节过的，所以我们所看到的分布只是原有分布按比例放大或缩小后的状态。假设位序-规模按比例放大或缩小了s倍，得出另一个位序sri（t），则位序规模比例扩大或缩小程度可表示为sPi（t）∝（sri（t））-1=s-1ri（t）-1∝ ri（t）-1∝Pi（t），说明无论数量级为多少，比例扩大或缩小的效果是一样的（Batty and Shiode，2003）。

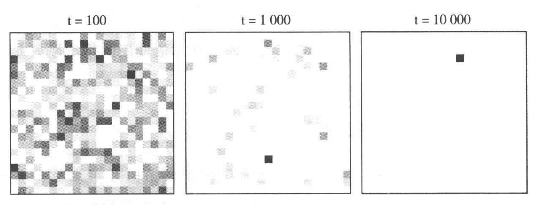
图5.2　设置阈值的比例效应模型下的位序-规模分布

设置最小值的比例效应就相当于带反射壁的随机游走（Sornette，2004；Saichev、Malevergne and Sornette，2010）。这一模型是极其简单的，因为它不包含对象之间任何形式的竞争和交流。这是极其奇怪的，因为城市之间充满了竞争和交流，而且许多关于城市形成的模型都强调这种交流。设置阈值的比例效应模型，其分布很明显是成比例的，而且符合齐普夫定律，但是在很多情况下，这个模型都是不稳定的。单纯看分布出现的时间以及高位序单位或者地区的波动性就可以知道这个模型并不能反映真实的状况，虽然我们在之前的章节中就已经讨论过波动性的问题而且经常有城市在很短的时间段里发生规模（当然也包括位序）的上下波动。但是仅仅规模分布与现实一致这一点并不足以说明这个模型就是个好模型。例如，随着时间的推移，分布产生的变化并不在于比例而在于它们的形态。这点表现在两个方面。在图5.2中，我们分别呈现了100次、1 000次及10 000次迭代后产生的分布图，随着迭代次数的增加，可以看出越来越明显的聚合趋势。在图5.3中，次数较少的迭代显示的分布相对次数较多的迭代显得更加平缓。

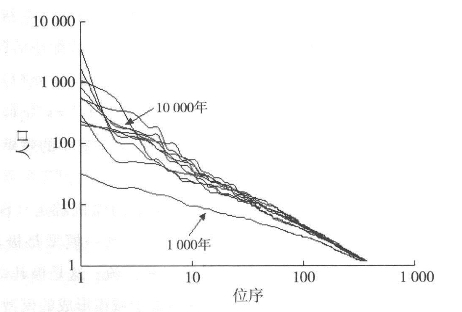
图5.3　随人口分布出现的幂律缩放

然而，随着t值的不断增加，当t=1 000，t=2000直到t=10000时，可以明显看出分布变得陡峭起来。这说明随着人口增长，参数γ也在不断变大。事实上，参数在向齐普夫所提到的统一靠拢，虽然仅仅凭这些数据并不能直接推导出这一结论。但是正如加贝克斯（1999）、布兰克和所罗门（2000）所指出的，大量的理论都说明了这就是带反射壁的随机游走带来的增加。在图5.3中，当t值由1 000上升到10 000时，每间隔1 000，参数γ的值分别为0.668、0.862、0.907、0.977、1.008、0.984、0.980、0.978、1.053和0.962。很明显，参数γ最后的取值在1上下波动，而且每个值的方差都达到了99%以上。这是一个非常显著的结果。这个没有涉及任何空间竞争的虚构模型产生了一个简单却高度有序的等级结构，这实际上印证了过去一百多年关于很多城市很多地区所汇集的实证数据。图5.4是美国一些行政地区从1970年（大约7 000个地区）到2000年（大约25 000个地区）的位序-规模图。图5.4a显示了整个分布，而且这个分布很明显是对数正态分布。当我们去掉短尾部分，剩下的长尾部分就相当于一条直线，也就对应了幂律法则。图5.4实际上是对应图5.1中理论模型的实证数据，而且对应从1970年到2000年的四个10年，γ参数分别为0.986、0.982、0.995和1.014。这四个值的方差与理论模型中的相比更小。法国学者格林-佩斯（Guerin-Pace，1995）也做过同样的动态分析，皮曼（Pumain，2006b）也给出了详尽的分析。

虽然这个模型所产生的分布总体上和我们在很多地区观察到的实证现象都很接近，甚至可以说是不可思议地接近，但是当我们仔细审视这个模型的时候，我们会发现它也并不如我们想象中的那么完美。事实上，这个模型存在着很多不一致性。其中，最需要引起我们关注的就是随单元位序变化而产生的结构上的不一致性。在“10 000年”的模拟实验中，有18个不同的单元曾经排位第一。而我们总共才采集了50个时间段的位序信息，所以很有可能在模拟的过程中有多于18个不同的单元曾经排位第一。为了更直观地了解位序波动的幅度，我们在图5.5中给出了第一、第六、第十二及第十八等高位序单元在10 000年中位序的变化。这些单元在不同的时间段都出现过，但是它们保持在高位序的时间却很短，这说明这个模型缺乏一定的连贯性。由于模型中的时间与现实世界毫无干系，因而也就无从得知模型中的“10 000年”对于现实生活中城市体系的演化，例如图5.4中美国城市体系的演化，究竟有何意味。正如我们在上一章中提及的，模型中分布波动的幅度比现实情况要大得多。(www.xing528.com)

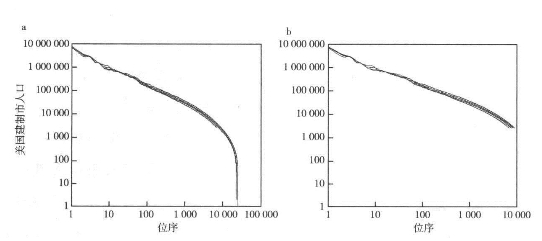
图5.4　美国建制市的人口幂律分布图和对数正态分布图

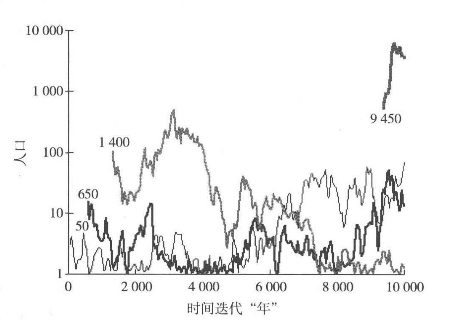
图5.5　位序第一、第六、第十二及第十八的人口单元及其在模拟实验中的发展

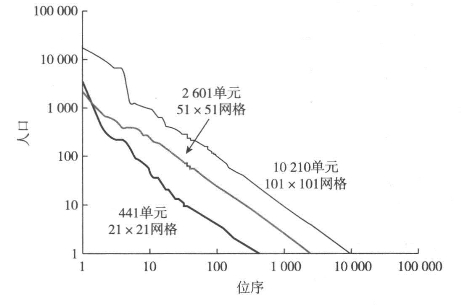
图5.6　不同规模网格具有比例一致性

在我们将空间交互作用与竞争纳入模型并对之加以完善之前，我们要最后观察一下改变模型空间地理维度可能带来的影响。我们首先将网格由21×21改为51×51，而后又改为101 × 101，然后通过设置阈值的模型进行了10 000年的模拟。图5.6中列出了三种情况下的位序-规模分布。显然，三种分布的斜率是相似的，说明当地理空间规模变大后，我们的模型也仍然适用。这一结果也是意料之中的，因为城市单元之间并没有任何交流，但是有趣的是随着体系规模的扩大，人口规模也在扩大。这有些奇怪，但或许是因为当空间系统扩大时，极端增长产生的可能性也会随之增大。当然，和模型的其他很多方面一样，这一点也需要进一步研究才能确定，但是这并不会影响模型在空间扩大后的适用性。令人称奇的是，这样简单的一个模型，我们费尽心神进行模拟和数学分析，却也无法彻底了解它。