人口呈现幂律分布的基本原因是边界之间交流的不对称，人口既不会呈现负增长，也不太可能不断膨胀。某种程度而言，幂模型并不能进一步解释交流不对称的情况，因而也只能是一种数学的构造。下一章我们将会看到，尽管这一模型展现了人口分布过程，城市规模增长时间跟现实生活中城市的变化并不相符。在我们开始考察经验证据之前，我们还需要更深层次的理论解释。接下去，我们就将探讨一种理论。
假设某一城市体系在时间点t的总人口固定为P（t），N个时间段人口总和为Pi（t），即：
城市规模发生变化的唯一途径来源于迁徙。我们设任一时间段［t→t+1］中城市移民为ΔPi（t），且0＜ΔPi（t）＜Pi（t）。如果我们假设一种最简单的情况，在随机选择的时间t内，随机选择的两个城市j和k之间发生的移民使得城市j在人口数量Pj（t）基础上增加ΔPj（t），而城市k则减少了相同的人口，方程可表示为：
方程4.10中的守恒也很容易被表示为：
这一过程就好像原子随机对撞中获得与失去能量（人口数），总能量（总人口数）则保持恒定。在一个系统中，两城市分别具有人口P1（t）和P2（t），两个人口事件分别为P（P1（t））和ρ（P2（t）），其相乘的概率为ρ（P1（t）+P2（t））=ρ（P1（t））ρ（P2（t））。因此，唯一符合标准的就只有玻尔兹曼分布律（Boltzmann-Gibbs distribution）ρ（P1（t））=C exp
，其中
为每个城市平均人口，C是比例常数（Dragulescu and Yakovenko，2000）。
这一结论适用于很多事件与城市，若稳态分布满足：
负指数分布与概率分布直接相符。如果我们用反向累积方式做积分运算，进而线性化并利用最小二乘回归法计算参数，我们也可以将其看作位序-规模分布。现在，设方程4.13为连续式方程，算
积分，回归到离散型方程，负指数分布类似的位序-规模分布方程可以被写成：
(www.xing528.com)
方程4.14可以被线性化成logri（t）=logK-λP（t）。为了与前文所定义的位序-规模关系保持一致，我们实际上将其写成：
其中很明显参数
。
至此，我们已经利用简单的资源交换模型建立起了分布方程，适用的参数包括N=500城市，总人口10 000，时间点总数为100万。我们从平均分布的情况开始，即每个城市有20人，固定每次增长或减少数为ΔPj（t）=2，∀j，t。模型开始运作后，我们确保人口数不少于零。如果我们选择的城市人口数小于零，直接放弃这组数据，重新选择城市，采纳人口数大于等于零的情况。如方程4.14所示，城市规模的分布逐渐导向玻尔兹曼律。我们在图4.3a中展示了概率分布，在图4.3b中展示了位序-规模对数模式，两者都证明与理论分布十分吻合。如德勒吉列斯库和雅科文科（Dragulescu and Yakovenko，2000）所示，概率分布在吻合度上略低于位序-规模分布，但原因主要是人为误差，如果计算次数接近100万，吻合度也会接近完美。每个城市的平均人口通过位序-规模分布中的斜率表示，这与各系数及交换模型的初始条件相符。尽管这并不是严格意义上的幂次定律，通过放宽条件，使用相同的代数，我们也可以看出交换—移民的过程会趋向幂次定律的分布。
图4.3 加性交换模型生成玻尔兹曼分布
注：a.频度到27的分布；b.全部范围的位序-规模分布。
在很多交换模型过程产生的人口规模分布会与等级-规模法则相符，乘性模型而不是加性模型会使得分布趋向幂律形态。然而，这些模型容易受到交换率和交换量的影响，并且它们无法保持系统中应有的人口总量。比如类似方程4.11所示，城市是随机选择的，并随机新增与城市人口成一定比例的人口数，并从随机选择的另一城市人口中去掉相同比例的人口。由于两个城市的人口基数并不相同，对称性就被打破了。
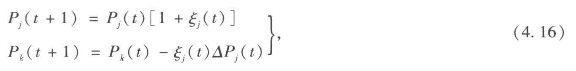
方程4.16中，我们设随机选择的变化率为ξj（t），且0＜ξj（t）＜1。只有当人口值小于1时，交换才会发生，也即若Pj（t），Pk（t）＜1，交换被放弃。如果我们大量进行此类交换，城市规模的概率分布将逐渐汇聚，但具体是哪种分布模式仍不清晰。举例来说，我们采用与上述玻尔兹曼律模型相同的起始参数，也即N=500城市，总人口10 000，时间点总数为100万，每个城市20人的统一分布。然后，使用总是小于0.5的随机变化率，分布将接近幂次定律，见图4.4所示的位序-规模模式。然而，当增长率更低时，其他模式更接近指数型。若人口数被作为资本或财富来考虑，即人口数可以为负值，又会有全新的模型。这些模型在其他研究中也曾被使用过（Ispolatov、Krapivsky and Redner，1998）。
图4.4 乘性模型生成类幂律分布
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
