简单递归模型展示出人口变化与增长率之间的通用增长方程

增长模型的基本假设是在任意两个时间段（t，t+1）之间，变化与目标（主体）的规模互成比例。如果城市发展随着时间推移而继续增长，那么两者就是正相关的。如果我们假设净增长率“λ”保持恒定，目标的变化，也即人口变化P与增长率之间的关系为

方程4.1中一个简单的递归所导向的回升或复合可以表示为：

该方程是通用的增长方程。从中我们很容易得知当λ＞0时，人口急剧增长；当λ＜0时，人口急剧下降；如果λ=0，人口保持恒定，也就是说P（t+T）=P（t）。如图4.1所示，我们可以看到关于此方程清晰的变化。然而，如果各个时间段的净增长率在-ξ＜λ＜ξ范围内随机变化，且平均净增长率为0，这一增长率将产生复合，人口从正值开始，增长率逐渐趋于0，人口最终也将归于0。当然，这也取决于增长率围绕0上下随机波动的次序，如果这一随机增长率自始至终均为正值，人口将呈现指数增长。这一原理可以用于解释一个较大的人口数量样本，比如城市系统中的人口。接下来，我们将进一步探究。通过图4.1我们发现，在我们选择的典型随机增长率出现次序下，人口下降到0。为了使人口在据其最初数值固定的范围内上下波动，我们需要引入加性模型（additive model）而不是乘性模型（multiplicative model），各个阶段的增长独立于之前的增长率。

似乎我们设计的人口模型和太多不同的目标相关，人口也似乎总是正增长的。而当我们将随机选择的增长率应用于每个不同的目标时，结果会不同。若随机增长率大于一个单位，结果是基数较大人口的小幅增长，而当随机增长率小于一个单位时，结果是基数较小人口的大幅增长。到这里，我们可以总结单个目标的模型为：

方程4.3递归的结果是在T点之后的长期方程：

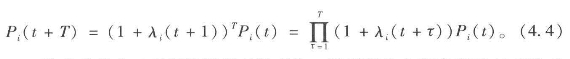
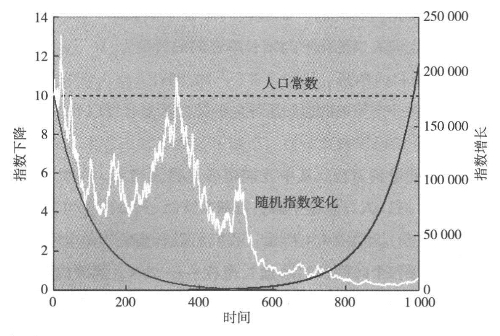
图4.1　指数变化

（黑色，连续增长；浅灰色，持续下降；连续常量虚线，下降；白色，随机变化）

这意味着人口规模将呈现对数变化。我们将此方程应用于10 000个城市，每个城市从一个单位的人口开始，并将随机选择的增长率λi（t）在-0.01＜λ（t）i＜0.01代入每个城市i。人口分布如图4.2a所示：显然，由于无人口规模的限制，人口分布向左倾斜，并随后表现为正态对数，甚至幂函数。经过10 000个时间单位之后，最大人口为12 119，但平均人口仅为9。实际上，对于模型的解读源自季布兰特（Gibrat，1931），他用此模型研究公司规模中比例效应与增长过程的关系。此后，该模型也被多次用于强有力地证明该过程与上述规模分布的关系（Sornette，2004；Saichev、Malevergne and Sornette，2010）。

布兰克和所罗门（Blank and Solomon，2000）发现，如果采用更小的约束值，比如在此次研究中保证人口数量不低于1个单位，分布将呈现为幂函数。图4.2a清晰地展示了如果我们使用f［Pi（τ）］，我们将得到(www.xing528.com)

K是比例的常量，α是分布的反幂。我们可以通过使预计值之间平方差的和最小化来拟合方程4.5，将参数K和α进行回归分析，从而将方程4.5转化为：

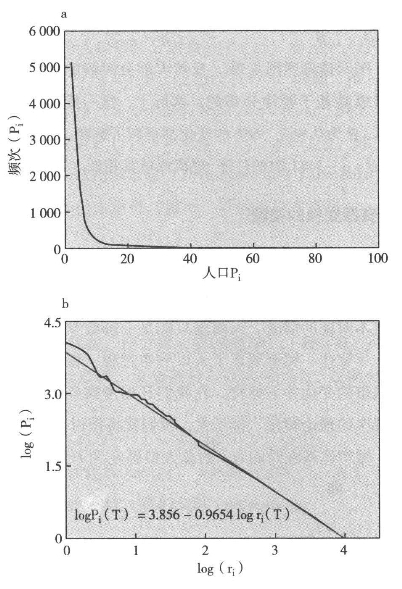
图4.2　比例增长

（a）频度范围100以内的分布，最大值为12000；（b）整个范围的位序-规模分布。

如果我们认为方程4.5是f（P）=KP-α的延续，我们求下界至上界的积分得出累计计数，这与r相等。在离散条件下，时间断面τ的人口位序Pi（τ）为：

当β=α-1（Adamic，2002），我们可以将其改写线性形式：

方程4.7是由齐普夫（1949）提出的位序-规模律，也就是我们在第1章中提到的定律，我们可以用以下方程表示：

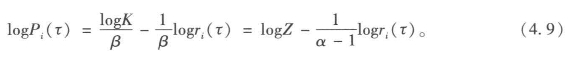
方程4.9图示请参照图4.2b，显然大部分时候的关系是线性的，也因此证明了规模是基于幂律分布的。实际上，这一模拟产生了几乎典型的幂函数关系，β为0.965，99%的变化都得到了解释。这与齐普夫定律也就是α=2且β=α-1=1时的位序-规模律极其相似（Zipf，1949）。