平面网络和二维图表：网络聚类更少见的空间结构

本书中我们并不是简单地关注存在于欧几里得空间中的网络或图形，而是关注具有不同的空间嵌入度的关系集。有些网络的节点是固定在特定地点上的，但它们的连接并不固定，比如航线、无线电，而与视线相关的网络，一直到社会网络，它们的节点和连接可能在持续地移动，而且肯定不与空间上的固定点有关。然而，所有我们将要分析的网络都有一些空间联系在其中，它们往往与城市和物质规划相关。本节我们将集中关注最严格的空间网络，其节点和连接都嵌入在空间中，比如街道网络。毫无例外的是，这些网络都从属于承载着我们在第2章介绍的那类流的基础设施，但是需要注意的是我们分析这些网络的方法，我们倾向于假设尽管它们的节点是固定的，它们的连接是抽象于其真实物质空间之外的。在某种程度上，这是我们处理这些系统的一种方法，而不属于它们在二维（或三维）空间中的真实运行。

实际上，我们将在这里提到的图或网络被称为“平面”，在不损失普遍性的情况下，我们将假定这种图是无向的。非正式地，这些图中的任意连接之间都没有焦点，是我们把它们表达在二维空间里。更正式地说，存在一个守恒规则表明，在这种图中的节点数量N减去边数E加上面数F等于2，所谓的面指的是由边围合起来的区域，即

最简单的二维图是树图，树图中没有面，简简单单由一串没有成环的边缘组成。更复杂的二维图是一系列节点的三元组（triple），即每个三元组gijgjkgki=1中有一个连通的组成部分。现在想象一张图，从两个节点gi和gj及它们俩之间的连接gij=1开始，然后建立另一个节点gk和新的连接gik=1和gjk=1，完成一个三元组。我们接着增加另一个节点gℓ，并将它与现有节点中的两个相连，以使连接不相交。这样，我们可以想象这个图按照一系列三元组扩展，建立一个六角蜂窝状的结构。很直观地可以看出，如果当gij=1时，我们把从一个节点到另一个节点的距离当作dij=1，那么这个图每次增加一个新节点，其增长的距离不会超过两个单位距离。即，图中的总距离D（N）可以定义为：

那么很明显，图中的平均距离收敛为一个常量，而每个节点的入度（或出度）的平均数同样也收敛为N→∞。这些结果适用于其他种类的二维图，可以看出每个节点的平均入度的最大值小于等于6，同时其度分布更像一个随机图；即图中没有幂律度分布，也不太可能出现大型枢纽（Barthelemy，2010）。

这适用于类似街道的网络，这种网络中很少出现超过6条或7条连接进入或离开的节点。当然，在网格模式中连接数平均为4，而且大多数街道网络的合理入度的范围可能遵循左偏态分布，其均值大约为4。对于轻轨网络和重轨网络来说，入度平均数更小；实际上，对于在世界城市中的一系列地铁系统来说，在它们的环线内，密集核心区的平均入度的阶为2.5（Roth、Kang、Batty and Barthelemy，2012）。实际上，在所有此类网络中，平面性倾向于理想化的结果，因为道路有时候并不相交而是通过隧道和桥跨越，铁路网络就是个明显的例子。甚至公共事业网络也按照这种方式相交，也许更甚，因为它们的选址比供给人和货物移动的网络更加灵活。对于信息网络来说，到目前为止我们对它的形态甚至拓扑结构都还没能形成清晰的认识，但如果我们能够把它们在二维空间上画出来，很可能发现大量的交叉。此外，与通过优先选择生成的、遵循幂律度分布的网络相比，这种平面的网络聚类更小也更少见。

图3.8展示了一个在伦敦内城中心区的密集街道网络，该图是一个6英里见方的街区（总共36平方英里，大约93平方千米）。我们简单地用节点来代表每个街道交口，用节点之间的连接来代表街道片段，从中我们注意到图中的二维图形有几个关键属性。原始图是有向的，由各个位置上的单向街道组成，有很多尽端节点，以及在交通灯、交叉口等位置分隔街道片段的节点。实际上，真实的网络表现远远超出一个纯粹的二维图，但因为我们的兴趣只在任意两个节点之间是否存在连接之上，我们不考虑方向。使用这些简化手段，N=22 260个节点中大约有52 448个连接或边缘。通过方程3.3的计算，其平均连通性很低，只有0.000106，这表明平均度（注意本图是对称的，入度和出度相等）NC（Ψ）=2.356。这个度分布非常简单，最大连接数为6，其中一个节点有1到6条连接的分布为［4，615，6，313，10，130，1，194，7，1］。

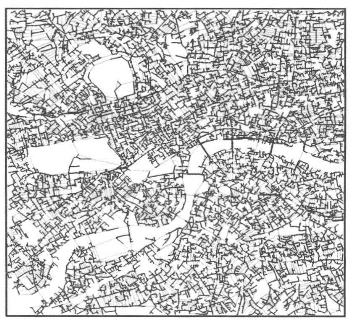
图3.8　伦敦中心街道二维图，图中最小生成树（图中最多）为黑线(www.xing528.com)

图中的总距离是边e的数量，由方程3.41可以计算出D=52 448。如果我们用图本身来计算它的实际距离，那么总距离是3 179千米，我们可以计算每段街道的真实平均距离为63米。与任意节点相关的平均距离，即到该节点最近邻点的距离除以所有这类距离的总数，为143米。在图3.9中，节点是任意排列的，我们把与每个节点相关的累计距离画为节点数量的增加（需要被连接的节点），可以看出这个距离与节点数成简单的线性比例增长，与节点所处的区域也呈线性关系。这个网络的最后一个值得注意的特性，是在图3.8中我们用粗线表示的最小生成树。该图表现了一个没有任何自环的二维图，所有节点都是相连的。因此这是个树图，而且它表现了穿越全图的更小的总距离（即到达每个节点）。当然，它并不是一个在伦敦这么密集的区域投递材料到每一个节点的高效系统，但如果材料必须从这些节点中的一个投递到另一个的话，它可能是一个高效的系统，正如我们对整个城市形态学的分析所能看出来的，我们将会在下文讨论。

图3.9　二维图中的累计距离

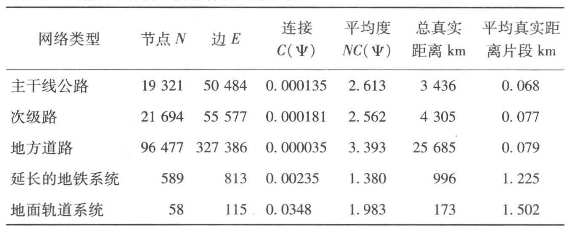
作为对二维图分析的总结，我们用相同的方法分析了大伦敦区域内的网络。图3.10a、3.10b和3.10c分别展示了这一网络大致按照容量，被分解为三个重要性层级，在3.10d中叠加了地铁和地面轨道网络。表3.1中列出了这些网络的不同测量值，可以清晰地看出道路指数明显聚集，但两种轨道网络与其他网络的区别很明显，在这类网络中树图更加适用。这些轨道网络的节点之间的平均距离远大于道路网络，而且它们的连通度更高，片段数量与可能的片段数量之间的相关性大于道路系统。实际上，尽管道路系统在三个不同的层级上，但它们相互之间很相似，连通度很低而所有的三个节点间的平均距离都小于100米。很明显，这是这些网络相交方式的一种加工，说明在包含高速公路和干线公路的主要道路级别，很少有立体交叉建设，因为大多数主要道路是从普通道路系统的不可或缺的部分逐渐演变而来的，这构成了当地交通的一个关键元素。

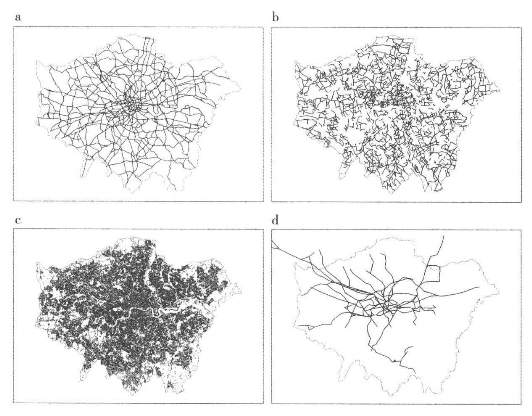
图3.10　大伦敦地区分级交通网络图

注：a.大伦敦地区内的高速公路和主干线公路。b.二级公路和次级路。c.大伦敦地区内的地方道路和路径。d.地铁和地面轨道网络。

表3.1　大伦敦地区内不同实体网络的特性

这一分析也表明，在出行过程中从一个网络切换到另一个网络的游客，他们的行为可能会受到这些网络之间的区别的影响。分析多模式切换及其对耦合网络的可能影响是网络科学领域的一项较大挑战，我们在这里不再展开。同时也要注意表3.1中的计算，地铁网络与第2章以及接下来部分所采用的计算方法不同，图3.10d中的网络是基于穿过相同站台的线路之间的连接，而不是之前使用的拓扑形式。这些网络表明我们需要更有效的方法来把它们连接在一起，但是因为我们还没有有效的方法来分析它们如何相交，如何共同发挥作用。第三篇的后面部分，我们将关注顺序耦合的网络，这将涉及解决冲突的问题，并引出“网络的网络”，但我们的科学并不会转到这一领域。