连通性、聚类和小世界：图形的不同极端

我们用于描述流和网络的许多工具和模型对于两种系统都适用，但流系统常常在结构上比网络更加同质化，因此我们在这部分介绍的大多数结构测度方法都是基于图形。简而言之，图形结构与连接的存在与否相关，尽管在很多流系统中，每一个连接都伴随着很多流，就像我们在上述例子中展示的那样。在某种程度上这也是一个比例问题，但我们将使用的方法关注的是连通性和聚类，只有当节点之间的可能连接的某个子集存在的时候这个方法才有意义。除了结构方法以外，网络科学最近的发展产生了很多关于节点和连接密度的统计学模型，我们将通过一些分析和统计分布，来完成我们关于结构方法的简单调查。

我们对图形的构成元素还没有下过严格的定义，很大程度上是因为这些术语会随着极少数强烈的惯例而改变。节点、枢纽、顶点都是用来定义图的元素或基本组成部分，连接、弧或边都可以用来描述元素间的联系。我们将在定义为G（N，g）的图形中使用节点和连接，其中N是节点的数量，gij是节点（或起点）i和节点（或终点）j之间的一条普通的连接。这与我们之前非正式的论述是一致的。我们已经定义了一个基本方法，将方程3.3的图的连通性定义为C（Ψ），即大于阈值Ψ的正二元连接与所有可能连接数的比例，如果可能的话，自连不计算在内。当然，这个方法可以归纳后用于不同的子图，而且在某种意义上，图中不同聚类的任意分区，都适用该连通性。最容易理解的包含节点的结构方法，是根据它们的度来定义的。一个节点的入度dj指的是前往该节点的连接数，定义为

而出度di则是以该节点为起点的连接数

这些是计算节点密度的方法，它与连通性的关系为：

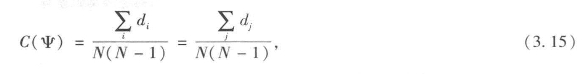
其取值为0到1。很容易可以看出，平均密度（或平均入度）可以计算为NC（Ψ），取值为1到N-1之间。

图的组成部分可以是一个节点或一组与每个其他节点都相连的节点，因此可以平均为一种超级节点。在一定程度上，当我们把图分解或者构成层级时，我们假设在每个层级上元素都是按照这种方式连接的，尽管它们可能并不是，因为通常会应用相似性标准，而层级是随着节点之间和节点组之间的相似性减少而建立的。在图3.7中，我们的层级实际上是基于完全连接的加权图建立的，这种加权图是具有与连接强度相关的相似性标准的流系统，而不是连接存在与否的情况。这直接为我们引出了适用于细分这个系统的一系列方法。最常见的一种是聚类分析法，其中，一个聚类被定义为基于一个特定节点i的完全连接的子图。对于有向图，我们基于gik计算所有在其附近的连接，因为∀k≠i，同时，我们建立这个数字与所有可能在附近存在的连接的比值。那么，最早由瓦茨和斯托加茨（Watts and Strogatz，1998）定义的聚类系数为(www.xing528.com)

其中，整个图的平均聚类系数可以计算为

注意，C与总体连通性指数C（Ψ）不同，但可能可以预料的是，它们是共变的，因为它们衡量的是类似的连接密度。

图形概念的核心是道路、路径和循环。途径包含一系列不需要区分的节点，然而路径是一个有清晰节点的漫游。循环是一个环形的道路，如果其节点是清晰的，它也有可能是一条路径。实际上，如果每个节点到另一个节点都存在路径的话，不管这个路径是有向的还是无向的，图形或多或少都是连通的。杰克逊（Jackson，2010）为这个领域提供了一个容易理解的导论，他引用了网络科学（Harary、Norman and Cartwright，1965）发展之前更早的概念。图论大部分针对的是图中路径的分析，但在这里，我们运用的主要不是这个，因为在第二篇中，我们关注的是流系统，在第三篇中我们会关注图示进程。然而，在网络科学中一个正在发展的领域通过这些方式研究城市网络，我们将在下面提到。

一个与图形规模的相关概念与任意两个节点之间的平均距离有关；这个特性构成了从规模和连通性的角度来定义不同类型图形的基础。假设每个节点有相邻点d，而每个相邻点与相连的相邻点之间的距离，就像在二元图中一样，为一个单位距离。在这类简图中，计算到达所有相邻点的平均距离十分简单，因为所有的节点所拥有的相邻点数相同，这里的相邻点指的是与任意节点i之间的步距或距离为1、2、3一直到n的点。注意，我们假设n是一个单位距离。那么，1个步距远的范围内有d-1个邻点，2个步距内有d（d-1）个邻点，3个步距为d2（d-1），总的来说，n个步距则有dn-1（d-1）个邻点。当到达一个数量级的时候，邻点的数量到达N～dn，因此我们可以把步距或典型距离计算为n=log（N）/log（d）。假设每个节点有100个相邻点，那么我们可以计算出到达比方说100亿个人的典型步距为5。实际上，这个值是图的直径，如果这是关于世界人口按照相互关系配置的合适模型，那么它直接展示了到达每个人的步距很小，实际上小于所谓的六度分离，这被称为“小世界”（Milgram，1967；Watts，2002）问题的特征。然而，这并不是一个合适的模型，因为人群转变为聚类，因此典型距离可能稍微有点大。

由密集的连通组群构成的图形的另一个极端是随机图。这类图由从总集N中随机选择出来的用于连接不同节点的弧组成，符合每对节点之间不超过一条连接的条件。在这类图中，任意一对节点之间的平均距离与节点数量之间的相关较小，但其聚类系数也小。金芳蓉和陆临渊（Chung and Lu，2002）展示了这类图中的平均单位距离或步长n取决于度分布，但在遵循幂律分布的图中，它可以和log［log（N）］一样小。在聚类图中，聚类系数很大，但平均距离也很大。实际上，许多社会系统呈现相对较小的路径长度和相对较大的聚类系数，反映出随机图和聚类图之间的某些折中。瓦茨和斯托加茨（1998）将这类图称为“小世界”，并且他们在按对数log（N）增长的图中展示了平均距离或步距n。近年来有很多在不同领域拆分许多网络结构的案例，都能够证明小世界（Watts，1999；Newman，2010）的存在。实际上，二维图不包含小世界，因为它们的平面性意味着由于欧几里得空间的特性，连接很少相互交叉，我们稍后会检验二维图，并将之应用在空间网络上。因此它们不能代表密集聚类。

网络科学中很大一部分的关注点不是在图的结构上，至少直接关注结构的很少，但会关注它们的统计特性，统计特性强调的是连接的分布，即起始或前往不同的节点。任意节点有d条连接的概率p是一个二项式，而且如果这个概率值小而节点数量大的话，那么其分布近似于泊松分布（Poisson distribution）。简而言之，很多这种度的分布接近正态分布。另一类网络在一定程度上处于另一个极端，它们之中的节点度呈偏态分布。节点很少但有很多连接，或者是有非常高的度，但是连接数很少。这些网络可以通过偏好依附的过程来建立，用这种方式建立的网络中，丰富的节点会变得更丰富，贫乏的节点则保持贫乏。巴拉巴希和阿尔伯特（Barabasi and Albert，1999）使用过这种方法，尽管在网络方面可以追溯到德索拉·普莱斯（de Solla Price，1965），而在此之前尤尔（Yule，1925）在随机系统方面有过应用。在本书中我们不会过多讨论网络形成的动力，但在第5章中，我们将探索这些网络是如何生成节点度上的偏态分布，并遵循幂律和比例。这会重新应用到第1章中介绍的比例法则，但我们仅在接下来的两章中认真谈论这个问题，首先讨论位置分布，然后讨论网络。

本章中我们将介绍网络的另外两个重要特性。我们首先关注的是进程，网络由进程所定义，然后我们会检验将网络植入空间系统中的方法，展示二维图与空间图的区别。网络进程可能有很多种，但所有进程都包含一个概念，即网络作为散布在节点之间的流的交流手段，是直接连通的。因此，网络可以生成叶栅流（cascading flow），如果节点或边在某些地方损坏了，叶栅流中的中断可以被找到，但进程还可以被定义为，当代理人运用不同的影响度或对其他对象的控制权的时候，进程是用于说明信息或想法或意见是如何被集中在一起的，即节点之间的冲突可以怎样被解决。这引出了反映交易、贸易或交换的互动网络的概念，我们将会在第三篇中详细介绍。在某种意义上，扩散是所有这些进程的核心，但在下一部分中，我们将关注网络中的交流如何实现冲突解决，其中包含作用于图的进程中的稳态或均势。正如我们会看到的，这是街道网络系统集中性的关键点，我们会在第6章和第7章中提到。在网络上把马尔科夫过程应用于意见池的想法，是我们在第三篇构建的概念的核心，第三篇中我们的关注点会转向为关键代理人和参与方是怎样就城市规划达成一致意见建模的方法。