二部图：流图与对偶图展示

二部图基于任意两个对象集之间的联系，或是对象与其他对象区分开来的本质属性。有时，在二部图的双模系统中，对象和属性指的是“模式”（Borgatti and Everett，1977）。在不加权的情况下，它们是从流矩阵中提取出来的，一般是具有NxM形式的关系矩阵｛Aik｝。严格来说，这类关系不是空间互动模式中的移动所构成的那种流，但可以方便地把它们当作存在于等价图形中，我们称之为Γik。我们可以在不失去二元图的普遍性的情况下，用数值Ψ阈值化矩阵｛Γik｝，类似我们对流矩阵｛Tij｝在方程3.2中所用的方法。那么

正如我们通过区分对象i或属性k的联系或不同来建立流矩阵一样，我们可以在这些数集之间建立高层级的流矩阵（从双模式减到单模式）。在对象的属性之间做比较的话，加权图Θij为

那么其对偶为

实际上，虽然Θij和Φkℓ是从二元二部图中建立起来的，但它们并不是二部图，如果再一次将它们阈值化，可以简化为以下形式：

其中合适的分割值为大于零的集。

这些流和二元二部系统在很多类的问题中出现，最早的应用可以追溯到70年前（Davis、Gardner and Gardner，1941）。在后续的章节中，我们将广泛地将它们用于对街道系统中的片段和交叉点进行表现和模型化，从而与空间句法联系起来（Hillier and Hanson，1984）。我们同样会把它们用于表达行动者之间的社会网络，这些行动者参与城市设计中有关冲突解决的问题，我们将在本书的第三篇着重介绍。它们用于在“Q分析法”（Atkin，1974）中表达和分析社会关系，也用在科尔曼（1973）的社会交换理论中。在网络科学里，瓦特（Watts，2002）把这种二部表达称为从属网络。然而，在这里说明它们的用途，我们要考虑基于空间互动流系统的网络，基于空间互动的流系统是我们上一章的重点，构成我们前面的案例。这类在起点和终点之间的互动矩阵可以看作单部图，但严格来说，它们是二部的，因为起点和终点是不同的对象集。

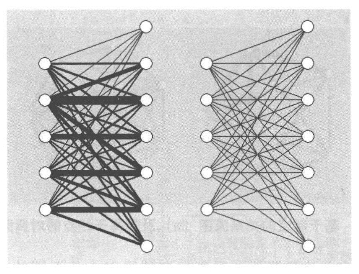
为了展示它们的用途，我们从大伦敦流数据集中选择了五个就业区作为起点，七个居住区作为终点。起点是大型内城就业区，终点的居住区也是另外两个内城区域。它们的具体位置在哪对于我们的观点无足轻重，但流矩阵｛Aik｝是由｛Tij｝的子集组成的到底意味着什么对于我们是有价值的。这个矩阵中的行是由流形成的，此处的流指的是从就业区到居住区的出行，接下来如果我们从通过终点的分布情况来建立每对起始点的关联或联系，那么方程3.4中的矩阵｛Fij｝就是衡量任意两个就业起点区在生成前往居住区的行程方面的相似程度的方法。正如方程3.8，把这个流矩阵的二部形式通过它的等价阈值转换为二元形式是很有用的。我们将其展示在图3.4中；我们没有在图中画出任何连接的箭头，但很明显的是，其隐含的二部图是有向的。如果这个矩阵中的两行是一样的，那么会出现相关系数等于1的情况。同样，如果我们比较任意两个终点的出行是怎样流向它们起点的，那么方程3.6中的对偶矩阵｛Hkℓ｝则是比较任意两个终点流向不同就业区的行程的相似度。这样，第一个矩阵衡量了就业区的相互关联程度，第二个则衡量了居住区的关联程度，但两者都是通过与对方的关系来衡量。如果每一个始点到它的终点的行程的分布形式都一样，那么这两个矩阵都会呈现相关系数等于1的情况。

(www.xing528.com)

图3.4　二部流图及其等价二元图

现在我们可以方便地展示如何建立流矩阵和它的对偶矩阵。我们用了方程3.4和3.6来计算，而不是用已经分割过的方程3.9和3.10。我们在图3.5a和3.5b（二部图中将流简化为线条表达）中展示了这两个矩阵。结果表明，如果我们对图3.5a中从起点到终点而后回到起点的流进行计数或者比较，对图3.5b反过来进行同样的操作，那么这些关系是对称的。实际上，当我们通过方程3.7计算关系矩阵，求得及其对偶等价值，这些都为这一对称性提供了显而易见的案例，见图3.6a和3.6b。它们提供了对这种模式进行分析和后续解释的基准，但需要注意的是它们关注的是互动模式，而不是简单的区位模式。

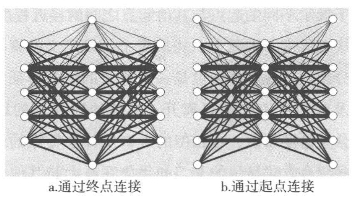
图3.5　连接二部图

实际上，很少有从这些方面来对城市互动进行的分析，为了展现我们的分析方法，现在我们将用伦敦的全部33个行政区（自治市）来检验整个行程矩阵｛Tij｝。为了进行这些比较，我们将计算基本二部流矩阵｛Aik｝内的元素之间的相对平方差，流矩阵｛Aik｝实际上是原始的行程矩阵，现在关注的是那些对象类型与终点十分不同的起点。考虑到两个从不同的起点（或终点）开始的大值之间的对比会比大值与小值之间的对比更加相似，我们并没有对这些平方差进行标准化。当然，其分布同样用这些平方差来解释，我们可以为起点和终点把平方差定义为

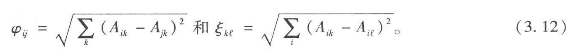
图3.6　基于起点的关系流图（a）及其基于终点的对偶图（b）

这些关系量度本质上是一个对象与另一个对象的不同程度的相异指数。它们太凌乱而不能像流图一样图形化表达，但我们可以把对象聚集起来，逐渐放松相似度，并在分类中增加更多的对象。图3.7a中的树图或系统树图用于展示不同的起点与其他起点之间的接近程度，图3.7b则展示了终点的接近程度。实际上，构成每个系统定义的聚类，它们的起点和终点都十分相似，这表明区位是一个重要的结构特征，决定了人们如何去工作以及如何从工作地点离开。虽然地理邻近的地区看起来集聚，但从因果分析角度来说，有相似的人口统计学特征的地区之间更接近。其实，这些组合方式显示的是，如果你在一个与其他地方相似的地方工作，那么这些地方与你居住的地方也会是相似的。这是一个复杂的问题，我们需要对空间互动系统是如何组织的，以及可能产生什么样的影响进行大量的思考。

图3.7　（a）起点基于终点流和（b）终点基于起点流之间的层级集聚差异