从流到网络：探究阈值对流图的影响

我们从起点i和终点j之间的流矩阵Tij开始，这一矩阵记录了两点之间的移动，如果用二维图^[1]来记录的话，这一矩阵可能被嵌入二维欧几里得空间中。让我们暂时不考虑空间，把这些起点和终点当成我们感兴趣的对象，比如个体、群体或者活动，这些对象可能是基于空间的，但很多时候并不是这样。正如我们在图2.1中把这些移动作为期望线画出来，我们在这里也用同样的方式将它们表示出来，但不标示它们在空间中的位置。我们将按照通常的表达方式，用特定的圆形网状图来表达流和网络连接，用圆上的点来表示枢纽或节点——起点和终点。然而，这种表达方式只有在起点和终点同属一类对象时才能采用，当它们不属于同类对象时，我们需要用二部图来表达。这一点我们将会在稍后进行讨论，现在我们讨论图3.1，基于图2.1中不同阈值的上班行程数据，我们画出了伦敦33个行政区之间的流。

实际上，我们画出了对称流，因为当节点超过10个的时候，很难用图形方法来表达网络中Tij和Tji之间的直接流。坦率地说，大多数网络，无论规模多大，在可能的情况下，都很难被梳理成看起来符合实际的关系图，因此，尽管我们以圆的形式来构建流图在某种程度上有点武断，但在缺乏非常明确的分级或聚类的情况下，我们仍然将以这种方式来表达流。因而图3.1是基于对称流Sij

图3.1　不同流阈的流、连接和网络

这组图显示，当我们选择不同的阈值，流图发生很大变化。图3.la表达的是完整的流矩阵；在图3.1b中我们仅画出连通性超过11 000的流，以表达所谓的强连接矩阵；而在图3.1c中表示的无连接矩阵中，在选择阈值时我们让节点之间完全断开，以形成两个或两个以上的独立系统。我们仍然是在分析流系统，但构成这些流的二元图（binary graphs）仅仅是节点之间连接的布局，我们在图3.1中的每种流图形的右边将这些二元图展示出来。因为这个矩阵是对称的，这些图不具有方向性。如果我们画出每一条单独的流，那么形成的图就具有方向性，我们将之称为有向图（digraph）。在本书的后续部分中我们将会用到这种图。

图3.1中的三组图分别展示了完全连接、强连接和无连接情况（Harary、Norman and Cartwright，1965）。在完全连接图中，从一个起点或终点发出的每个流都会直接到达其他每一个节点。在强连接图中，这样的流直接或间接地到达每个起点或终点，间接到达即通过中间节点到达。而在无连接图中，至少有一个从某个节点发出的流没有到达另一个节点，实际上将该图分为两个或更多的子图。这里有另外一种类型我们需要注意，称为弱连接图。这种类型的图中，每个节点都和其他节点相连，但任意两个节点之间都不可能找到直接路径。因此，弱连接图相比强连接来说连接要弱，但在我们引入的大多数模型中，我们的关注点会在对称和强连接的系统上，主要是因为这类科学处在初级阶段，并且在节点之间的连接方向上很难做到精确。

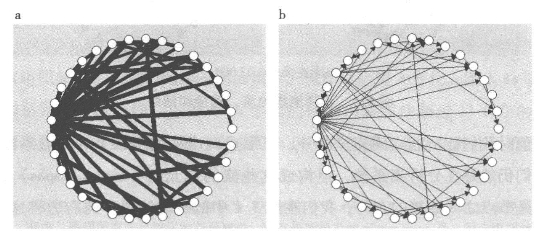
从我们的例子中，我们可以通过设定流的阈值来展示一个弱连接的系统。这是基于试错法，图3.2就是一个例子。该图十分稀疏，图中的箭头表示方向。我们把阈值设定在最大直接流的38%左右，此时所有节点仍然是系统的组成部分，但穿过整个图的路径数量很少。实际上，这是这个流系统高度不对称的间接证据。正如我们将看到的，这类流系统很少被作为图检验，因此对应了流和网络之间的分离，这一点我们会在继续阐释这一科学的过程中尝试解决。

(www.xing528.com)

图3.2　直接流和表示弱连接系统的图

我们关注的是把连接作为一种看待移动和互动的通用方法，这一关注点会直接引出一个问题：我们所检验的各类结构是怎样连接的。正如我们将会看到的，这类方法有很多，但我们值得通过一个集聚指标来考察，在密度降低时流系统及其图形会如何变化。最简单的方法就是计算图中存在的连接数量，并计算该数值与所有可能连接的比例。让我们定义一个一般图形G（N，g），其中节点为N，连接数为g。这与它相关的流系统T是相反的，流系统T中当节点（或起点）i到节点（或终点）j之间有流Tij时，gij才存在。如果我们将流阈值设定为Ψ，那么我们可以将图形中的二元关系定义为

连通性C（Ψ）为

在这种特定的方法中，我们不把自流Tii考虑在内；因此gii=0，∀i。连接的最大总数是所有节点之间其他可能的连接数，这取决于节点数量N。这种方法中的C（Ψ）的取值为0到1之间，当所有节点之间都存在连接时，C（Ψ）=1，这种情况如图3.1a所示的流矩阵，当系统中不存在流或整个系统完全无连接时，C（Ψ）=0，也就是说没有一个节点与其他任意一个节点有联系的简单情形。

这是非常简单的，但它提供了与网络进化相关的直接结构性结果，而且实际上它也与网络动力学相关（Watts，2002）。如果我们逐渐加大流的阈值Ψ，连通性会逐渐减少，由于底图组成系统的连接越来越少。我们可以识别出来系统从强变弱直到变成无连接的模式的那个临界点，这种情况下流的路径可能会有点出人意料。我们将用两种方法来分析伦敦数据，首先从完全连接图的所有连接都是正数时开始——即C（Ψ）=1时——然后按照从流量最小且只存在一条流的情况开始到流量最大的顺序，一条一条地减少流。我们在图3.1中的对称流矩阵中做了这样的处理，在图3.3中我们展示了这些方法中的两种。首先，我们简单地记录作为相连结构的一部分的剩余节点数n（Ψ）≤N，即强连接或弱连接的情况，然后我们会马上看到，当连接逐渐被去掉的很长一段时间里，系统仍然保持强连接，而后突然变成无连接。这里我们不用这种方法，但是当我们追踪成果图中的最短路径时，这些路径在无连接结构中的距离是无穷大，但会突然变为有限距离，然后迅速汇集到一个相对稳定的值。一旦超过这个阈值，简单地增加更多的连接并不会显著减少这些路径的长度。这是一个阶段转变的例子，在这一过程中系统迅速从无连接转变为有连接。我们在其他情况下检验了这个问题，但这种情况主要取决于网络的结构（Batty，2005）。更通常的情况下，不是用减少连接的方式来证明，而是逐渐在一个系统中增加连接，逐步增加到那个让系统突然变为连接系统的那个点，这个点是一个关键阈值，许多在无连接系统中不可能的活动和移动在这里成为可能。在某种意义上，这种类型的转变是一个简单的模型，模拟了城市如何从突然认识到规模经济效应的不连接组团开始发展的过程。图3.3实际上展示了伦敦案例的这一转变，尽管这一模型并不反映大城市地区的流系统实际发展。

图3.3　从完全连接到无连接的转变