流的势能对流场数据的计算

在前一节中，我们用交互风形式验证了势能，在考虑起点和终点的系统中生成了代表平均流向的加权向量。当起点和终点有很大差别，以上班通勤流为例，主要流向反映了这种差异，在像伦敦这样有单一强核心的城市，流明显地从就业起点中心到居住终点中心移动，具体如图2.3。如果我们假定起点和终点相同，并且流量矩阵是对称的，那么这应该会形成起点和终点矢量流的同一模型。我们所期待的线性图（图2.1）对其做了假定，就如同方程2.46和2.47中托布勒的对称基线重力模型一样。为了论证这一基于对称性的一般模式，我们建构了对称的平均流量矩阵方程2.57，并且在方程2.6中转换这个平均值为加权的概率性的流量矩阵，如方程2.58所示。

i、xi、yi和j、xj、yj的坐标区域对应了对称的流的方向，通过利用和方程2.7一样的位移方式而产生。我们在此重复一下，关于起点可写作方程2.59，终点为2.60 。

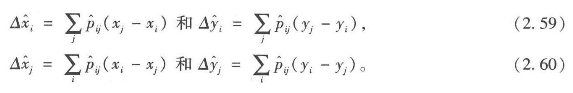
根据方程2.57和2.58，我们可以清楚地看到基于这些位移的起点和终点的向量是同一的，即方程2.61，

图2.9a反映了根据这些方程所计算的大伦敦地区的地图。我们需要注意，具有显著对称性的流的方向，很可能是由居住地而非工作地所决定的，反映出伦敦的主要流方向是从郊区到中心。

我们简要地介绍一下托布勒的第二个模型，它采用了相反的方法，用于构建非对称的流矩阵，如方程2.62：

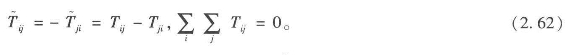
由于不对称性可正亦可负，将常量化更加困难，虽然这种差异更应被视为方向差异，而不是绝对差异。因此我们可以常量化方程2.62，形成权重而不是概率，得到方程2.63：

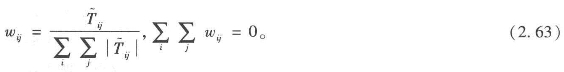
现在起点地区和终点地区坐标不同，由与方程2.7相同形式的位移生成，我们可将其写作方程2.64：

(www.xing528.com)

对于终点地区可写作方程2.65：

在大伦敦地区流量矩阵中我们计算了起点和终点的向量的不对称性，这些分别呈现在图2.9b和2.9c中。起点的梯度是背向中心的，然而终点的却是指向中心的，正如我们对此类单中心城市系统的预期。

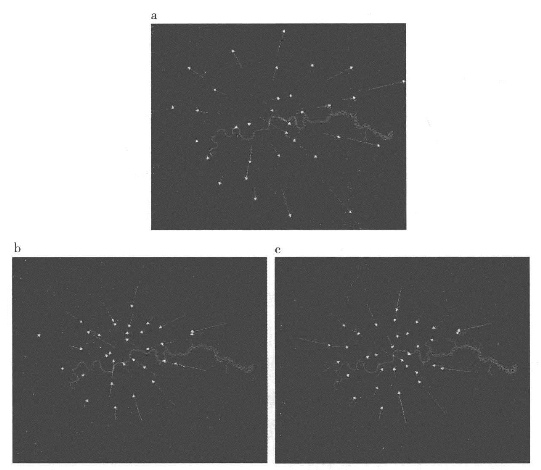
图2.9（a）定向的对称流（b）从起点处不对称的流（c）从终点处不对称的流

值得注意的是托布勒（1981）的非对称流动的具体模型，他认为应该用传统的对称的重力模型方程2.13进行建模。将流Tij模拟为：

如果模型是准确的，那么就没有不对称，那么。如果我们对j区的方程2.66求和，那么我们得到方程2.67：

现在，正如我们所预料的那样，这种势能可能不等于另一个其他的考虑到起点和终点或者在起点和终点的净差额，Δi不等于零。将起点和终点的对称吸引点记为Ai和Aj，托布勒认为可以将方程2.66近似为一个新的方程：

如果我们对方程2.68求和，代入j或i，我们可以写出净差额的方程2.69。

也有可能从净差来求解吸引点Ai然后去划分这些吸引点并且去检查它们的梯度。这是一个比我们这里的解释说明更为正式的互动风的概念扩展。但是总的来说，这可能更近似一种方向向量，我们可以通过使用方程2.69的答案计算出图2.3和2.9中的数据。虽然在这一章我们没有校准我们的数据模型，如果进行校准的话（详见第9章），我们将能够基于本章展示的大量模型变量对流进行预测并生成方向向量。