模型构建：无约束平台对买家进行价格补贴，对卖家盈利

采用标准的Hotelling模型分析框架，考虑市场上存在两个双边平台企业k（k＝A，B），分别位于线性城市[0，1]的两端，每个平台企业面临两组不同的用户i（i＝1，2），在线段上均匀分布，且每边的用户规模均标准化为单位1（记边1用户为买方，边2用户为卖方）。两平台企业都希望能有更多的用户在本平台上进行交易，并为此而展开竞争。假设两平台给予两边用户的内在收益vi足够大，以至于线段[0，1]上的用户都至少到一个平台上进行交易。假设买方可在平台间自由选择，是部分多归属的，而卖方是完全单归属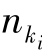，表示用户在平台上的单归属数量，而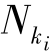表示用户在平台上的归属数量，包括单归属和多归属。令买方的一个用户距离平台A的距离为x，另一个用户距离平台A的距离为y，此时，两平台上买方单归属的净效用分别为：

而买方多归属的净效用为：

同理，两平台上卖方的净效用分别为：

其中，αi≥0表示双边用户间的交叉网络外部性强度，其含义为平台一边用户给另一边用户带来的外部效用（平台每增加一个买（卖）方时，卖（买）方所增加的效用），ti表示两边用户到平台上的平均运输成本，可视为交易平台对两边用户提供服务的差异化系数（t1、t2＞0），表示平台向两边用户收取的注册费。

为了保证买方为部分多归属，而卖方为完全单归属的双边市场以及市场均衡解的存在与合理，还需要有如下假设：

（1）t1＜α1＜2t1；（2）t1 t2＞α1α2和8t1t2－6α1α2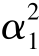－－＞0。

其中，假设（1）保证买方为部分多归属，而卖方为完全单归属；假设（2）确保利润函数πi是凹函数，并存在纳什均衡解。

由于两边用户在线段[0，1]上均匀分布，在x处，买方多归属和在平台A上单归属所获得的净效用相同，在y处，买方多归属和在平台B上单归属所获得的效用相同，即，于是有，

求解式（5.4），可得两边用户在平台上单归属的需求函数为：

为了简化计算，便于分析，假设平台服务两边用户的成本为零，则两平台的利润函数分别为：

将式（5.5）代入式（5.6），分别用平台利润函数对价格求一阶偏导可得，买方部分多归属而卖方完全单归属的情形下，双寡头平台竞争实现均衡时，对两边用户的定价分别为：

平台两边用户单归属的数量分别为：(www.xing528.com)

均衡时，两平台企业的利润相等且为：

从上面的式（5.7）可知，当卖方的网络外部性α2较强时，说明平台上每增加一个买方给卖方带来的效用较卖方给买方带来的效用更高，此时，平台有补贴买方的激励，即当平台实现利润最大化均衡时，平台可对买方制定低于边际成本的价格，甚至是负价格或提供直接的价格补贴，现在提出以下假设，

假设5.1

可验证，此情形下意味着α1＜α2，＞0。本章的目的是研究当不允许设定负价格时，平台将如何采取策略规避约束。那么，当非负定价约束绑定时，两平台对买方的定价为＝0，即对买方提供免费服务。同时平台对卖方的定价也相应做出调整，以保证双边用户加入平台进行交易。

平台受非负定价约束，记ρA，ρB为平台A、B的非负约束算子，用两平台的利润函数对价格求一阶偏导，可得：

当＜0，且非负定价约束绑定时，平台对买方的定价为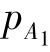＝＝0，而平台对卖方定价的最优反应函数为：

此时，ρA＝ρB＞0，因此，非负定价约束下，平台对两边用户的对称均衡价格分别为：

两边用户的单归属数量分别为：

实现均衡时，两平台获得的利润相等且为：

命题5.1　买方部分多归属而卖方完全单归属的情形下，双寡头平台竞争实现均衡时，受非负定价约束的两平台企业A、B，与无约束情形相比，对买方的价格上升，对卖方的价格下降，且买方的用户规模减少，卖方的不变，即

由上述分析可知，平台在边1市场定价受约束。需要注意的是，虽然平台提高价格p1减少了买方的用户规模，但也减了少平台在买方的损失。与无约束情形相比，可以看出，假设5.1下，无约束平台对买方的定价为负，对买方进行价格补贴，而对卖方的定价为正，平台的利润为正。而受非负定价约束时，平台对买方的价格升高，对买方实施免费服务，对卖方的价格降低，平台的利润增加。下面研究平台企业如何利用捆绑销售策略放松非负定价约束，扩大服务用户的范围，从而实现对用户隐性的价格补贴，使得平台盈利。