一元线性回归分析结果及统计推断

以【例2】说明一元线性回归分析模型.

【例2】某化学反应中温度x与产品的产出率y的观测数据如表3-8所示，试研究y与x的回归关系.

表3-8

（1）作散点图.

以温度x为横坐标、产出率y为纵坐标，将表3-8中数据（xi，yi）画成散点图，如图3-28所示，y与x近似存在线性关系.

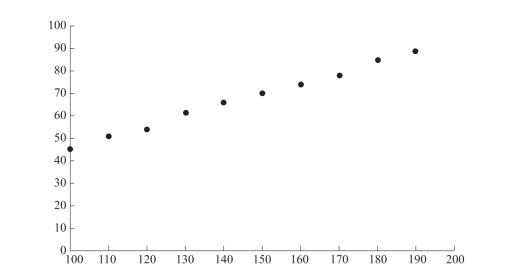
图3-28

（2）确定回归方程.

在进行回归分析前先输入数据，如图3-29所示.单击“数据”→“数据分析”→“回归”→“确定”按钮，弹出“回归”对话框，如图3-30所示.

图3-29

图3-30

在“Y值输入区域”输入B1：B11，表示B列第1行至第11行因变量y的数据，在“X值输入区域”输入A1：A11，表示A列第1行至第11行自变量的数据.因为第一行为表头，所以在对话框的“标志”处打“√”，“置信度”打“√”（默认的95%或者根据需要改为其他百分比）；“输出选项”可选“新工作表组”；“残差”项目可选，也可不选；“正态概率图”一般不选.单击“确定”按钮，得回归分析结果如图3-31所示.

图3-31

由图3-31得回归系数=-2.7393939， =0.48030303，所以回归方程为

“回归统计”中主要项目解释如下：

（1）Multiple R：相关系数r，其值r≤1，越接近1，线性关系越显著；

（2）R Square：相关系数r的平方，越接近1，线性关系越显著；

（3）Adjusted R Square：调整后相关系数r的平方，永远小于相关系数r的平方；

（4）标准误差：均方差的估计值.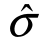

“方差分析”中主要项目见图3-32，具体解释如下：

（1）df：统计量所服从的2χ分布的自由度；

（2）Qe：残差的平方和，，和是回归系数；

（3）2=Qe /（n -2）：总体X的方差σ2的无偏估计.

图3-32　方差分析表的主要项目

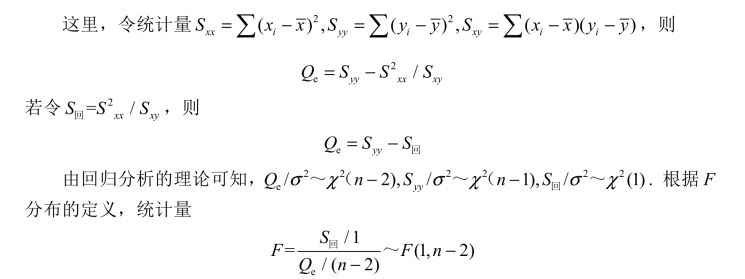
如果y与x的线性关系越好，则Qe 越小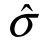，2也越小，F值越大，回归效果越显著.

如果给定α=0.05，查F分布表得临界值Fα（1，n-2）=F0.05（1，8）=5.318.若F＞Fα，则回归效果显著.本例中F=2131.564远大于Fα，所以回归效果显著.

习 题 3.9

某物流快递公司每月的总运输量x（单位：万吨）对总成本C（单位：万元）的数据如下，试给出C和x的回归关系.

章节测试三

一、填空题

1.设随机事件A和B互不相容，P（A）=0.2，P（A∪B）=0.5，则P（B）=________.

2.从1，2，3，4，5中任取三个数字，则这三个数字中不含1的概率为________.

3.已知A和B相互独立，P（A）=0.2，P（B）=0.6，则P（AB）=________.

4.对于相同的置信度，置信区间的长度越小，估计的精度越________（高/低）.

二、选择题

1.设随机事件A和B互不相容，且P（A）＞0，P（B）＞0，则________.

2.某人连续向一目标射击，每次命中目标的概率为，他连续射击直到命中为止，则射击次数为3的概率是________.

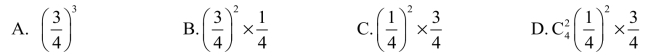
3.设随机变量X～B（4，0.2），则P{X＞3}=________.

A.0.001 6

B.0.027 2

C.0.409 6

D.0.819 2

4.已知随机变量X和Y相互独立，且它们分别在区间［-1，3］和［2，4］上服从均匀分布，则E（XY）=________.

A.3

B.6

C.10

D.12

5.在假设检验问题中，显著性水平α的意义是________.

A.在H0成立的条件下，经检验H0被接受的概率

B.在H0成立的条件下，经检验H0被拒绝的概率

C.在H0不成立的条件下，经检验H0被拒绝的概率

D.在H0不成立的条件下，经检验H0被拒绝的概率

三、计算题

1.甲、乙两人独立地向一目标射击，已知甲击中目标的概率为0.6，乙击中目标的概率为0.5，求目标被击中的概率.

2.从发芽率为0.999的一批种子中随机抽取500粒，进行发芽试验.计算500粒种子中没有发芽的比例不超过1%的概率.

3.设甲袋中有3个红球、1个白球，乙袋中有4个红球、2个白球.从甲袋中任取一个球（不看颜色）放到乙袋中，再从乙袋中任取一个球，问取到一个红球的概率是多少？

4.公共汽车门的高度是按成年男子与车顶碰头概率在0.01以下设计的，设成年男子身高X服从正态分布，且μ=170cm，σ=6cm.问车门高度应定为多少？

5.设随机变量X的概率密度为

求：（1）E（X）；（2）D（X）.

6.某种电子管的使用寿命服从正态分布，从中随机抽取15个进行检验，计算得均值为1 950 h，标准差为300 h，试以95%的置信度估计整批电子管平均寿命的置信区间.

7.假定考生成绩服从正态分布，在某地一次数学考试中随机抽取了36位考生的成绩，算得平均成绩为66.5分，标准差为15分.求在显著性水平0.05下，是否可以认为这次考试全体考生的平均成绩为70分？

8.某地区女孩年龄和平均身高之间存在线性相关关系，统计数据为

(www.xing528.com)

求：（1）女孩身高关于年龄的线性回归方程；（2）进行线性相关的显著性检验（α=0.05）.

综合测试一

一、填空题

3.设随机变量X～N（-1，4），则E（2X）=________，D（2X）=________.

4.A、B、C构成一个完备事件组，且P（A）=0.5，P（B）=0.3，则P（C）=________.

二、选择题

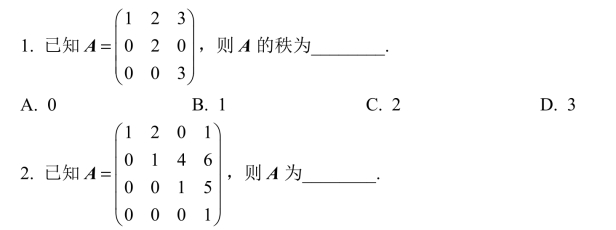
A.单位矩阵

B.对角矩阵

C.上三角形矩阵

D.下三角形矩阵

3.设总体X～N（μ，σ2），其中μ已知、σ2未知，若（X1，X2，X3）为来自总体X的一个样本，则下列表达式中不是统计量的是________.

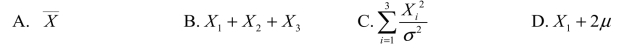
4.A与分别代表一个线性方程组的系数矩阵和增广矩阵，若这个方程组无解，则________.

5.下列对立事件表达错误的是________.

A.掷一枚硬币，A=“出现正面”，=“出现反面”

B.在含有3个次品的100件产品中任取5个，A=“至少有一个次品”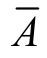，=“全是正品”

C.甲、乙两人进行乒乓球比赛，A=“甲胜”，=“乙胜”

D.掷一颗骰子，A=“出现的点数小于3”，=“出现的点数大于4”

三、计算题

4.袋中有5个红球、3个白球、2个黑球，求任取3个球恰好为一红、一白、一黑的概率.

5.成年人中吸烟的占25%，吸烟的人得肺癌的概率为0.18，而不吸烟的人得肺癌的概率仅为0.01，求一成年人得肺癌的概率.6.设随机变量X的概率分布为

求：（1）E（X）；（2）D（X）.

7.假设某厂生产的一种钢索的断裂强度为X（单位：kg/cm2），且X～N（μ，402），从中选取一个容量为9的样本，数据（单位：kg/cm2）如下：775，776，779，779，780，780，782，784，785，能否根据此样本认为这批钢索的断裂强度为800 kg/cm2（α=0.05）？

综合测试二

一、填空题

二、选择题

A.单位矩阵

B.对角矩阵

C.方阵

D.数量矩阵

3.设总体X～N（μ，σ2），其中μ，σ2是未知参数，若（X1，X2，X3）为来自总体X的一个样本，则下列表达式中不是统计量的是________.

4.A与分别代表一个线性方程组的系数矩阵和增广矩阵，若这个方程组有无穷多组解，则________.

5.设A、B、C表示三个随机事件，若三个事件中至少有一个发生，则下列表述正确的是________.

三、计算题

4.一批零件共50个，次品率为10%，每次从中任取一个，取后不放回，求第三次才取得正品的概率.

5.两台车床加工同样的零件，第一台加工后的废品率为0.03，第二台加工后的废品率为0.02，加工出来的零件放在一起.已知这批加工后的零件中第一台加工的占，第二台加工的占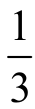，求从这批零件中任取一件得到合格品的概率.

6.设随机变量X的概率分布为

求：（1）E（X）；（2）D（X）.

7.某一化肥厂采用自动流水生产线，装袋记录表明，实际包重为X，且X～N（100，22），打包机必须定期进行检查，确定机器是否需要调整，以确保所打的包不会过轻或过重.现随机抽取9包，测得数据如下：96，97，99，101，102，103，105，107，108，若要求完好率为95%，问机器是否需要调整？

综合测试三

一、填空题

1.(3x2+2x)′=________.

2.∫cosxdx=________.

3.设随机变量X～N（0，1），则E（-2X-3）=________，D（-2X-3）=________.

4.A、B、C构成一个完备事件组，且P（A）=0.5，P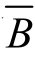（）=0.7，则P（）=________.

二、选择题

3.设总体X～N（μ，σ2），其中μ，σ2是未知参数，若（X1，X2）为来自总体X的一个样本，则下列表达式中是统计量的是________.

4.A与分别代表一个线性方程组的系数矩阵和增广矩阵，若这个方程组有唯一解，则________.

5.三支考签由三个考生轮流有放回抽取一次，每次取一支，设Ai（i=1，2，3）表示“第i支考签被抽到”，则“至少有一支考签没被抽到”表示正确的为________.

三、计算题

4.袋中有18个白球、2个红球，从中随机地连续取3个球，取后不放回，求第三个球是红球的概率.

5.设某批产品中，甲、乙、丙三厂生产的产品分别占45%、35%、20%，各厂的次品率分别为4%、2%、5%，现从中任取一件，求取到次品的概率.

6.设随机变量X的概率分布为

求：（1）E（X）；（2）D（X）.

7.糖厂用自动打包机打包，已知包重X（单位：kg）服从正态分布，即X～N（μ，σ2），且σ2=1.每包标准质量为100 kg，每天开工后需要检查一次打包机工作是否正常，即检查打包机是否有系统偏差.某日开工后测得9包质量（单位：kg）如下：99.3，98.7，100.5，101.2，98.3，99.7，99.5，102.1，100.5，问打包机工作是否正常（α=0.05）？