回归分析中的显著性检验：r²值对线性关系的影响

1.相关系数

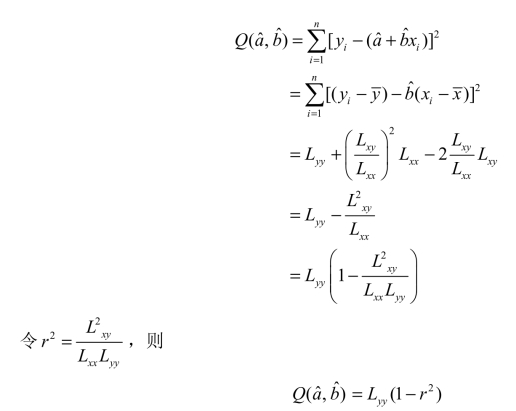
而Q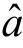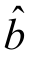（，）≥0，Lyy ≥0，所以1-r2≥0，从而-1≤r≤1.

因为Q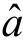（，）=Lyy （1-r2），当变量y与x的样本值（xi，yi ）（i=1，2，3，…，n）确定以后，只有r2的值决定Q的变化，r2的值越接近于1，Q的值越小，变量y与x之间的线性关系也就越显著；反之，若r2的值越接近于0，Q的值越大，变量y与x之间的线性关系也就越不显著，用回归直线来表示变量y与x之间关系就越不准确.r的值可以表示变量y与x之间具有线性关系的相对程度.

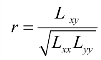（-1≤r≤1）称为变量y与x的相关系数.

当r=±1时，Q=0，所有的样本值（xi，yi ）（i=1，2，3，…，n）都落在直线上，称变量y与x完全相关；当r=0时，Q的值最大，说明变量y与x不相关或是非线性相关关系.

2.线性相关的显著性水平检验方法

一般地，按照以下步骤对线性相关的显著性进行检验.

（1）提出原假设H0：y与x的线性关系不显著，记b=0.这是因为当b=0时，回归直线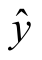 =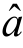+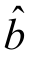x是一条平行于x轴的直线，无论x如何变化，y的值均为常数.显然，不可能有显著的线性关系.

（2）选用统计量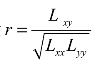，并根据样本值计算r的值.

（3）按给出的显著性检验水平α 和自由度f=n-2，查附表5的相关系数检验表，得临界值λ.

（4）作出判断.

当时，则拒绝原假设H0，说明变量y与x的线性关系显著；

当时，则接受原假设H0，说明变量y与x的线性关系不显著.

【例 2】某建材实验室做陶粒混凝土实验时，考察每立方米混凝土的水泥用量（单位：kg）对混凝土抗压强度（单位：kg/cm2）的影响，测得数据为

（1）求经验回归方程；（2）检验一元线性回归的显著性（α=0.05）.

解 （1）将计算列成表格，如表3-2所示.(www.xing528.com)

表3-2

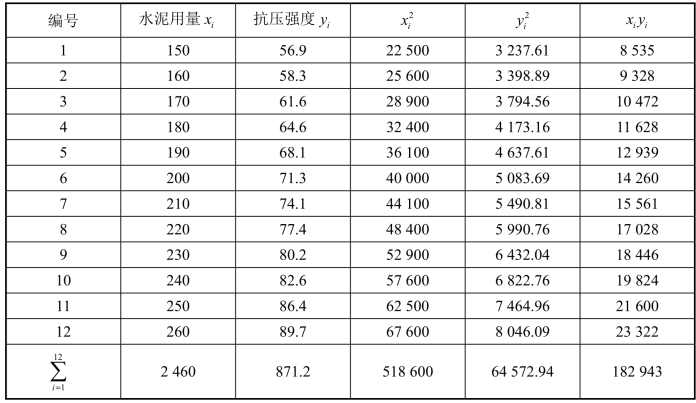
由表3-2可得

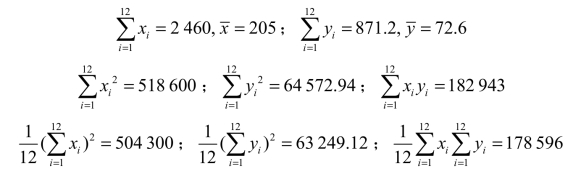
代入数据得

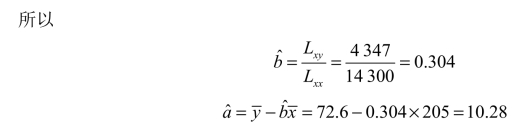
故经验回归方程为

（2）提出假设H0：b=0.

由给定的显著性水平α=0.05，自由度f=12-2=10，查表得临界值λ=0.576.

因为，所以拒绝原假设H0：b=0，即变量y与x存在显著的线性相关关系.

习 题 3.7

1.根据统计数据，某10年间世界制造业的总产量年增长率x（单位：%）与世界制成品总出口量年增长率y（单位：%）的变化关系为

求这两个变量的线性回归方程.

2.根据统计数据，某地耐用消费品销售额y（单位：百万元）与居民人均月收入x（单位：元）关系密切，相关资料为

（1）求经验回归方程；（2）检验一元线性回归的显著性（α=0.05）.