【摘要】：设在一次试验中，取得n对数据（xi，yi），其中yi是随机变量y对应于xi的试验值，图3-19中的直线是根据这n对数据（xi，yi）描绘的回归直线，其中是试验值yi的回归值.图3-19每一个试验值yi与回归值i之间的差为yi-i，在图中表示为两个纵坐标之差，这个差有正有负，其绝对值为.但由于绝对值在处理上比较麻烦，所以一般用平方和表示，即这个平方和Q是随着回归系数，而变的，因此它是，的一个二元函数
设在一次试验中，取得n对数据（xi，yi），其中yi是随机变量y对应于xi的试验值，图3-19中的直线是根据这n对数据（xi，yi）描绘的回归直线，其中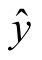
是试验值yi的回归值.
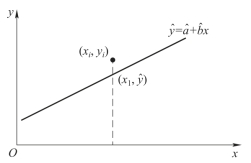
图3-19
每一个试验值yi与回归值
i之间的差为yi-
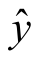i，在图中表示为两个纵坐标之差，这个差有正有负，其绝对值为
.但由于绝对值在处理上比较麻烦，所以一般用平方和表示，即
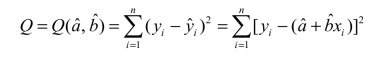
这个平方和Q是随着回归系数
，
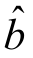而变的，因此它是
，
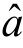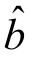的一个二元函数，其中xi，yi 为常数.
根据二元函数求极值的方法，求偏导数并令其等于0，得
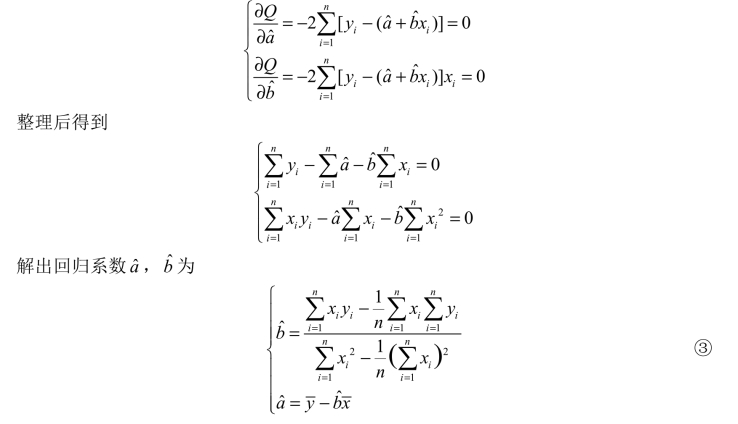
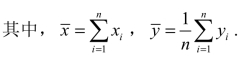
式③还可写成
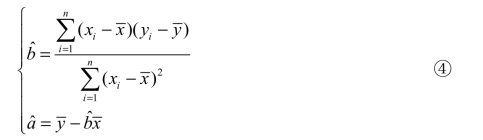
式中，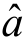
，
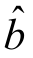即为Q的最小值系数，使得
达到最小.
以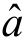
，
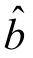为回归系数的直线方程，就是我们所要求的回归方程，它最能代表这些点的散布状态.由于在求系数
，
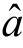时，是使平方和Q最小，故称这种方法为最小二乘法.
如果令
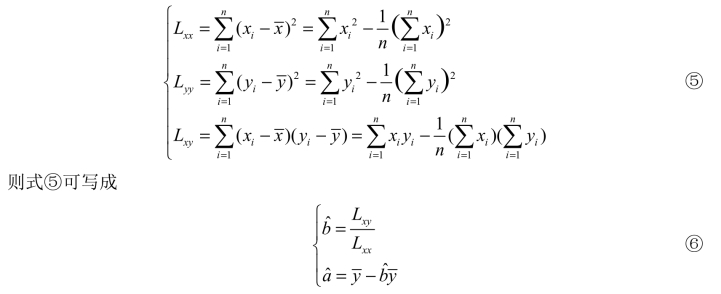
将求得的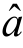
，
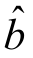代入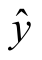
=
+
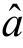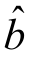x，就得到一元线性回归方程的具体表达式.(https://www.xing528.com)
【例 1】写出引例中总成本C对运输量x的回归方程.为了方便起见，借助计算机，将计算列成表格，如表3-1所示.
表3-1
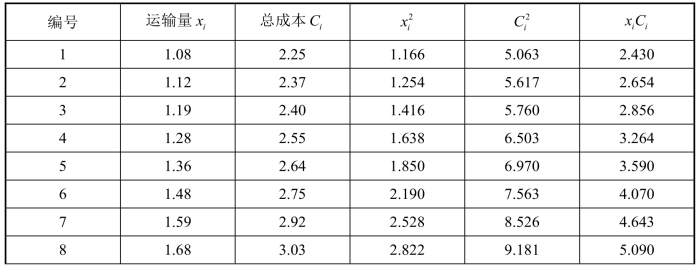
续表
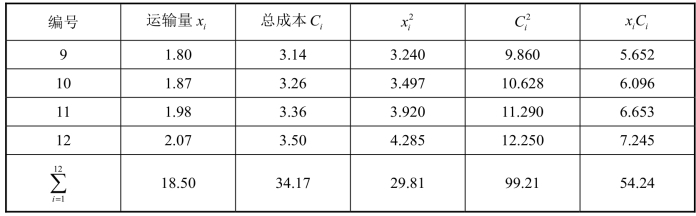
由表3-1可得
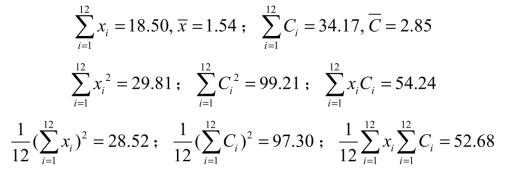
代入数据得
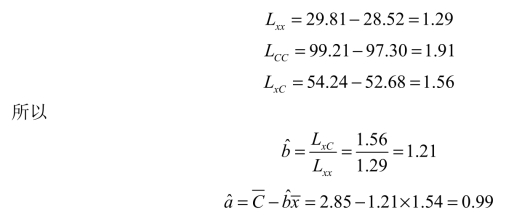
故总成本C对运量x的回归方程为
从中可知固定成本为0.99万元，可变成本为1.21万元.
结合例子我们求出了一元线性回归方程，下面归纳一下具体步骤：
（1）由题中经验数据，列出回归方程计算表；
（2）由公式计算回归系数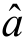
，
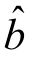，把
，
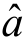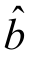的值代入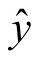
=
+
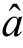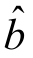x，即得回归方程.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
