参数区间估计：置信区间的定义和含义

区间估计

1.置信区间的概念

定义5 设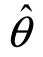（1X1，X2，…，Xn）及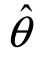（2X1，X2，…，Xn）是由样本观察值确定的两个统计量，如果对于给定的概率1-α，有

则称随机区间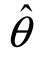（1，2）为参数θ的双侧置信区间，称1-α为置信度（或置信概率），称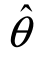1、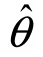2分别为双侧置信区间的置信下限和置信上限.

这种估计未知参数的方法称为参数θ的区间估计.

置信区间的含义：在随机抽样中，若重复抽样多次，则得到样本X1，X2，…，Xn 的多个样本观察值x1，x2，…，xn，对应于每个样本值都确定了一个置信区间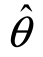（1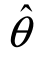，2），每个这样的区间可能包含或不包含θ的真值.根据大数定律，当抽样次数n充分大时，这些区间中包含θ的真值的频率接近于置信度1-α，即在这些区间中包含θ的真值的区间大约有n（1-α）个，不包含θ真值的仅占nα个.例如，给定1-α=0.95，重复抽样100次，其中大约有95个区间包含θ的真值，大约有5个区间不包含θ的真值.

置信区间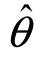（1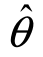，2）也是对未知参数θ的一种估计，区间的长度意味着误差，故区间估计与点估计是互补的两种参数估计.

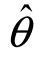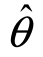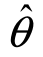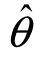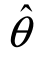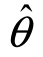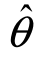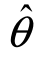置信度与估计精度是一对矛盾.置信度1-α越大，置信区间（1，2）包含θ的真值的概率就越大，区间（1，2）的长度就越大，对未知参数θ的估计精度就越差；反之，对参数θ的估计精度越高，置信区间（1，2）的长度就越小，（1，2）包含θ的真值的概率就越低，置信度1-α就越小.

2.求置信区间的步骤

寻求置信区间的基本思想：在点估计的基础上，构造合适的含样本及待估参数的函数U，且已知U的分布，再针对给定的置信度导出置信区间.

一般步骤如下：

（1）选取未知参数θ的某个较优估计量；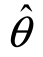

（2）围绕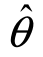构造一个依赖于样本与参数θ的函数U=U（X1，X2，…，Xn，θ）；

（3）对给定的置信度1-α，确定λ1和λ2，使

通常可选取满足P{U≤λ1}=P{U≥λ2}=的λ1与λ2，在常用分布的情况下，由附表查得；

（4）对不等式λ1≤U ≤λ2作恒等变形后化为

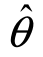（1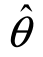，2）就是θ的置信度为1-α的双侧置信区间.

（θ，θ）就是θ的置信度为1-α的双侧置信区间.

3.单正态总体的置信区间

1）正态总体方差2σ已知，参数μ的置信区间

设总体X～N（μ，σ2），其中σ2已知，μ为未知参数，（X1，X2，…，Xn）是取自总体X的一个样本.

对于给定的置信度1-α，可查标准正态分布表求出使

因此，均值μ的置信度为1-α的置信区间为

【例5】2020年，一场突如其来的新冠肺炎疫情使得国民经济受到了一定冲击，为了促进消费，恢复国民经济，现调查当地居民的平均消费额，随机访问了100名居民，得知平均消费额=80（单位：元）.根据经验，已知居民消费服从正态分布，且标准差σ=12（单位：元），求该地居民平均消费额μ的置信度为 95%的置信区间.

解 本题是正态总体的方差已知，对总体均值μ进行区间估计，故选择统计量

对于给定1-α=0.95，α=0.05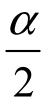，=0.025，查表得U0.025=1.96，代入置信区间公式，得置信区间为

所以，该地居民平均消费额μ的置信度为95%的置信区间为（77.6，82.4）.

【例6】 已知某药品中某成分的含量X在正常情况下服从正态分布，X～N（μ，0.1082）.现测定9个样本，其含量均值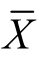=4.484，试估计药品中这种成分含量的总体均值μ的置信区间（置信度为0.95）.

解 本题是正态总体的方差已知，对总体均值μ进行区间估计，故选择统计量为

当1-α=0.95时，α=0.05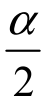，=0.025，查表得Uα2=U0.025=1.96.已知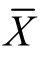=4.484，代入置信区间公式，得置信区间为(www.xing528.com)

所以，药品中该成分平均含量在置信度为0.95时的置信区间为（4.41344，4.55456）.

2）正态总体方差2σ未知，参数μ的区间估计

设总体X～N（μ，σ2），其中μ，σ2未知，（X1，X2，…，Xn ）是取自总体X的样本.

对于给定的置信度为1-α，可查t分布表求出使

成立的临界值±tα2（n -1），由

因此，均值μ的置信度为1-α的置信区间为

【例7】对某型号飞机的飞行速度进行 16 次试验，测得最大飞行速度样本均值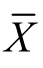=425，样本方差S2=72.052.已知最大飞行速度服从正态分布，试对最大飞行速度的数学期望作置信度为0.95的区间估计.

解 本题是正态总体的方差未知，对总体均值μ进行区间估计，故选择统计量

当1-α=0.95时，查t分布表得tα2（n-1）=t0.025（15）=2.1315.已知X=425，S2=72.052，代入置信区间公式，得置信区间为

所以，最大飞行速度的均值的置信区间为（386.6，463.4）.

【例8】某地九月份的气温X～N（μ，σ2），观察9天，得X=30，S=0.9，求置信度为0.95的此地九月份平均气温的置信区间.

解 本题是正态总体的方差未知，对总体均值μ进行区间估计，故选择统计量

当1-α=0.95时，查t分布表得tα2（n-1）=t0.025（8）=2.306，代入置信区间公式，得置信区间为

所以，该地九月份平均气温的置信度为0.95的置信区间为（29.3082，30.6918）.

3）总体方差的区间估计

设总体X～N（μ，σ2），其中μ，σ2未知，X1，X2，…，Xn 是取自总体X的一个样本.

对于给定的置信度1-α，可查χ2分布表得到双侧临界值，使得

所以，方差2σ的置信度为1-α的置信区间为

而标准差σ的置信度为1-α的置信区间为

【例9】某厂生产的钢丝，设钢丝折断力X服从正态分布，现随机抽取10根检查，样本均值=575.2，S2=104.3，α=0.05，求钢丝折断力方差的置信区间.

解 本题是对正态总体方差2σ进行区间估计，故选择统计量

所以，钢丝折断力方差σ2的95%置信区间为（49.3455，347.6667）.

习 题 3.5

1.为测试灯泡使用寿命，抽样10只灯泡测得寿命（单位：h）如下：1 458，1 395，1 562，1 615，1 351，1 490，1 478，1 382，1 536，1 496.试估计灯泡总体的平均使用寿命和寿命的标准差.

3.从一批钉子中抽取16根，测得长度（单位：cm）如下：2.14，2.10，2.13，2.15，2.13，2.12，2.13，2.10，2.15，2.12，2.14，2.10，2.13，2.11，2.14，2.11.设钉子长度服从正态分布，已知σ=0.01，求钉子平均长度μ的置信度为95%的置信区间.

4.某工厂滚珠车间，由经验可知，滚珠直径X服从正态分布，即X～N（μ，0.052）.现从生产的滚珠中任取6个，测得直径（单位：mm）如下：14.9，14.6，15.1，14.8，15.2，15.1.求滚珠平均直径的置信度为0.95的置信区间.

5.一家制衣厂收到150颗大衣红色纽扣，规定直径为10 mm，现随机抽取9个样本，测得直径（单位：mm）如下：9.9，10.9，10.0，10.1，9.9，10.1，10.0，10.0，9.9.假设纽扣直径服从正态分布，求μ的置信度为95%的置信区间.

6.岩石密度的测量误差服从正态分布，随机抽取12个样品，得标准差S=0.2，求σ2的置信区间（α=0.05）.