点估计
1.估计量与估计值
定义1 若θ是总体X的待估参数,用样本(X1,X2,…,Xn)的一个不含任何参数的样本函数![]() 来估计θ,称
来估计θ,称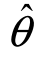 为参数θ的估计量;用样本的一组观察值(x1,x2,…,xn)可计算出估计量
为参数θ的估计量;用样本的一组观察值(x1,x2,…,xn)可计算出估计量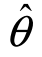 的相应值
的相应值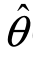 (x1,x2,…,xn),称为参数θ的估计值,记作
(x1,x2,…,xn),称为参数θ的估计值,记作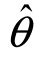 .
.
估计量是样本函数,具有双重含义:既是一个随机变量,又是估计量的观察值.对于不同的一组观察值,估计值一般是不同的.
定理1 样本均值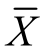 作为总体分布的数学期望μ的估计量,样本方差S2作为总体分布的方差2σ的估计量,即
作为总体分布的数学期望μ的估计量,样本方差S2作为总体分布的方差2σ的估计量,即
【例1】为估计一批木材的横纹抗压强度,随机抽取10个进行试验,得数据如下(单位:N/cm2):482,493,457,471,510,446,435,418,394,469.试估计这批木材横纹抗压强度的均值和方差.
【例2】为测试某仪器中的电子元件的使用时间,设总体X服从指数分布,其概率密度为
其中λ未知.抽取容量为5的样本值为1 002,1 004,1 005,998,996,试用点估计法估计λ的值.
2.估计量的评价标准
估计量是用来估计某个未知参数的,随着抽样的不同,得到的样本值也不同,估计量的值也会发生变化,故一次的估计值不足以评价估计量的优劣.因此对于估计量的选择,总是希望在多次估计中能够在被估参数的真值附近波动,且波动尽可能小.这样对一个估计量的好坏,有以下三种评价标准.
1)无偏性
定义2 设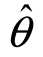 (X1,X2,…,Xn)是未知参数θ的估计量,若E(
(X1,X2,…,Xn)是未知参数θ的估计量,若E( )=θ,则称
)=θ,则称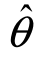 为θ的无偏估计量.
为θ的无偏估计量.
在科学技术中,E(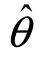 )-θ为
)-θ为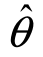 估计θ而产生的系统偏差,无偏性是对估计量的一个常见而重要的要求,其实际意义是指估计量没有系统误差,只有随机偏差.例如,当用样本均值作为总体均值的估计时,虽无法说明一次估计所产生的偏差,但这种偏差随机地在0的周围波动,对同一个统计问题重复使用不会产生系统误差.
估计θ而产生的系统偏差,无偏性是对估计量的一个常见而重要的要求,其实际意义是指估计量没有系统误差,只有随机偏差.例如,当用样本均值作为总体均值的估计时,虽无法说明一次估计所产生的偏差,但这种偏差随机地在0的周围波动,对同一个统计问题重复使用不会产生系统误差.
定理2 设X1,X2,…,Xn是取自总体X的样本,且E(X)=μ,D(X)=σ2,则样本均值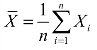 与样本方差
与样本方差![]() 分别是μ和σ2的无偏估计量.(https://www.xing528.com)
分别是μ和σ2的无偏估计量.(https://www.xing528.com)
【例3】某工程公司对桥梁进行维修,对某一距离进行5次测量,结果如下(单位:m):2 781,2 836,2 807,2 765,2 858.已知测量结果X服从正态分布,即X~N(μ,σ2),试求参数μ,σ2的无偏估计量.
2)有效性
定义3 设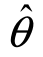 1(X1,X2,…,Xn)及
1(X1,X2,…,Xn)及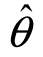 2(X1,X2,…,Xn)都是未知参数θ的无偏估计量,若
2(X1,X2,…,Xn)都是未知参数θ的无偏估计量,若
则称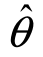 1比
1比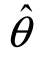 2有效.如果对于给定的n,在θ的一切无偏估计量中,D(
2有效.如果对于给定的n,在θ的一切无偏估计量中,D(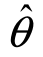 )的值最小,则称
)的值最小,则称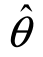 是θ的有效估计量.
是θ的有效估计量.
注意: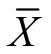 和Xi都是μ的无偏估计量,但是
和Xi都是μ的无偏估计量,但是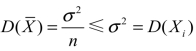 ,所以样本均值较个别观察值Xi有效.实际上,样本均值
,所以样本均值较个别观察值Xi有效.实际上,样本均值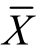 是总体均值μ的有效估计量.
是总体均值μ的有效估计量.
【例4】设X1,X2是来自正态总体X~N(μ,1)的样本,下列三个无偏估计量
哪一个最好?
解 计算三个无偏估计量的方差:
其中,D(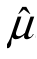 2)最小,所以
2)最小,所以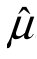 2比
2比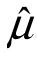 3和
3和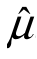 1有效,即
1有效,即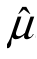 2是三个无偏估计量中最好的一个.
2是三个无偏估计量中最好的一个.
3)一致性
定义4 设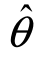 (X1,X2,…,Xn)是未知参数θ的估计量,如果随着样本容量n的增大,
(X1,X2,…,Xn)是未知参数θ的估计量,如果随着样本容量n的增大,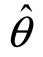 总能充分地趋近于θ,即对于任意ε>0,总有
总能充分地趋近于θ,即对于任意ε>0,总有
则称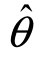 为参数θ的一致估计量.
为参数θ的一致估计量.
根据大数定律可得![]() ,所以样本均值X是总体均值μ的一致估计量.
,所以样本均值X是总体均值μ的一致估计量.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




