常用统计量的分布及其性质分析

1.样本均值的分布

定理4 如果总体X～N（μ，σ2），且（X1，X2，…，Xn ）是来自总体X的样本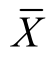，为该样本的样本均值，则

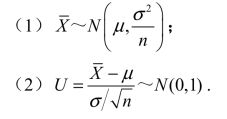
注意：当总体X～N（μ，σ2）时，不论样本容量n为多大，都有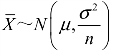.如果总体X不服从正态分布而服从其他某种分布，按照中心极限定理，当样本容量n充分大时，样本均值近似地服从正态分布.

定义4 如果U～N（0，1），对于给定的正数α（0＜α＜1），满足P{U＞λ}=α的点λ的值，称为标准正态分布的右侧临界值.

标准正态分布的右侧临界值的几何意义：临界值λ右侧的面积为α，临界值左侧的面积为1-α，即P{U＞λ}=1-P{U ≤λ}=α，P{U≤λ}=Φ（λ）=1-α，如图3-11所示.

例如，当α=0.01时，1-α=0.99，查标准正态分布表有Φ（2.33）=0.99，所以λ=U0.01=2.33；当α=0.05时，1-α=0.95，查标准正态分布表有Φ（1.645）=0.95，所以λ=U0.05=1.645.

定义5 如果U～N（0，1），对于给定的正数α（0＜α＜1），满足的λ的值称为标准正态分布的双侧临界值.

标准正态分布的双侧临界值的几何意义：临界值±λ左右侧的面积均为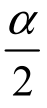，由右侧临界值定义可得P{U≤λ}=Φ（λ）=1-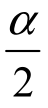，即λ=Uα2，如图3-12所示.

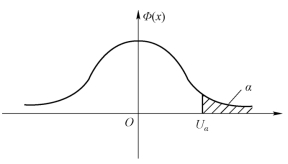
图3-11

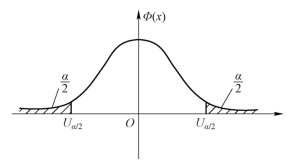
图3-12

【例3】某厂检查钢丝绳的承重能力记为X，且X～N（62，52）（单位：kg）.试问从中随机地抽取20根进行测定，其样本均值X低于60 kg的概率有多大？

所以，样本均值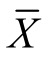低于60 kg的概率为0.036 7.

2.χ2分布

定义6 设总体X～N（0，1），（X1，X2，…，Xn ）是来自X的一个样本，称

为服从自由度为n的χ2分布，记作χ2～χ2（n）.

注意：自由度是指上式中所包含的独立变量的个数.

χ2（n）分布的概率密度为

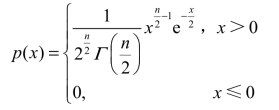
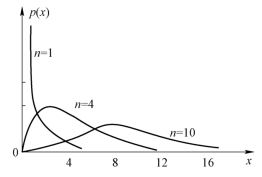
图3-13

定义7 如果χ2～χ2（n），则对于给定的正数α（0＜α＜1），满足P{χ＞λ}=α的λ的值，称为χ2（n）分布的右侧临界值.

χ2（n）分布的右侧临界值的几何意义：临界值λ右侧的面积为α，临界值左侧的面积为1-α，该临界值记作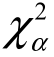（n），如图3-14所示.

例如，当α=0.01，n=6时，查χ2分布表有χ2分布的右侧临界值为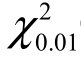（6）=16.812；当α=0.05，n=8时，查χ2分布表有χ2分布的右侧临界值为（8）=15.507.

定义8 如果χ2～χ2（n），则对于给定的正数α（0＜α＜1），满足P{λ1＜χ＜λ2}=1-α的λ1和λ2的值，称为χ2（n）分布的双侧临界值.

由图3-15可知，选择λ1、λ2分别使得在这两点左右部分的面积各为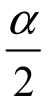，查表可得(www.xing528.com)

例如，当α=0.05，n=10时，查χ2分布表有χ2分布的双侧临界值为

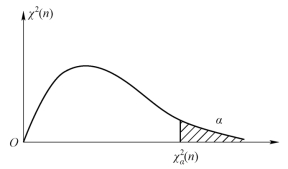
图3-14

图3-15

3.t分布

定义9 若X～N（0，1），Y～χ2（n），且X与Y相互独立，则称统计量

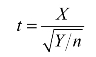
为服从自由度为n的t分布，记作t～t（n）.

t（n）分布的概率密度为

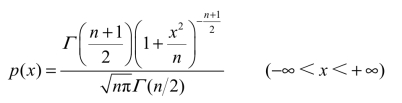
如图3-16所示，t（n）分布的概率密度曲线位于x轴上方，单峰且关于x=0对称，很像标准正态分布的概率密度曲线.可以证明，当n充分大时，有p（x）→φ（x）.

定义10 如果t～t（n），则对于给定正数α，满足P{t＞λ}=α的点λ的值，称为t（n）分布的右侧临界值.

定义11 如果t～t（n），则对于给定正数α，满足P{|t|＞λ}=α的λ的值，称为t（n）分布的双侧临界值，如图3-17所示.

例如，当α=0.05，n=18时，t分布的右侧临界值为t0.05（18）=1.7341，t分布的双侧临界值为±t0.02（518）=±2.1009.

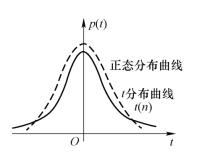
图3-16

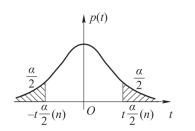
图3-17

定理6 若（X1，X2，…，Xn ）为来自正态总体X～N（μ，σ2）的一个样本，则

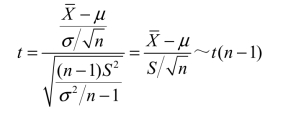
习 题 3.4

1.设总体X～N（μ，σ2），其中μ， σ2未知.X1，X2，X3是取自总体X的一个样本，试判断下列函数是否为统计量.

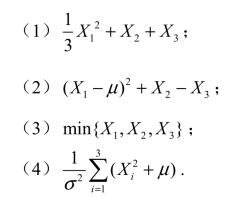
2.为了考核银行工作人员的业务能力，现对银行10名工作人员的办卡业务时间进行测试，测试结果如下（单位：s）：126，125，124，120，116，117，121，123，121，121，试求：（1）样本均值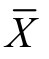；（2）样本方差S2；（3）样本的标准差S.

3.查表求下列各分布的右侧临界值.

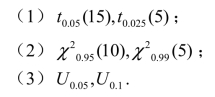
4.假设对敌人的防御地区进行100次轰炸，每次轰炸命中目标的炸弹数是一个随机变量.已知其均值为2，方差为1.69，求在100次轰炸中，命中炸弹数在180～220之间的概率.

5.正态总体X～N（3.4，62），随机抽取容量为n的样本，要使样本均值落在1.4～5.4之间的概率不小于0.95，问样本容量n至少应该多大？