数理统计：样本均值与离散程度之间的理论关系

1.大数定律

定理1（切比雪夫大数定律）如果随机变量X1，X2，…，Xn 相互独立，且具有相同的数学期望和方差：E（Xi）=μ，D（Xi）=σ2，（i=1，2，…，n ），那么对于任意的ε＞0，都有

此定理表明：在给定的条件下，当n充分大时，n个独立随机变量的平均数与这个随机变量分布的离散程度是很小的.这为我们提供了有关算术平均法则的理论依据，例如，为确定某一零件的长度，在相同的条件下进行了n次重复测量，每次观察值不尽相同，那么，究竟采用哪一次观察值作为长度真值的近似值呢？依据切比雪夫大数定律，应以所有观察值的平均值作为零件长度真值的近似.

定理2（贝努里大数定律）如果nA为n重贝努里试验中事件A发生的次数，p为每次试验中事件A发生的概率，那么对于任意的ε＞0，有

此定理表明：随着试验次数n的增大，随机事件A发生的频率在它的概率附近摆动，并且只要试验次数n足够大，事件出现的频率便会相当接近概率.也就是说，在重复试验中随机事件频率稳定在它的概率附近.

2.中心极限定理

一般来说，如果某一项偶然因素对总和的影响是均匀的、微小的，即没有一项起特别突出的作用，那么就可以断定描述这些大量的、独立的偶然因素的总和的随机变量是近似地服从正态分布的.这是数理统计中大样本的理论基础，用数学形式表达就是中心极限定理.

定理3　如果随机变量X1，X2，…，Xn 相互独立，服从相同的分布，且E（Xi）=μ，D（Xi）=σ2，（i=1，2，…，n ），则随机变量之和近似地服从正态分布，即X（n）～N[E（X（n）），D（X（n））]，由于(www.xing528.com)

即X（n）～N（nμ，nσ2）（近似地）标准化变换后，有

所以，对于任意实数x，有

此定理的实际意义：如果一个随机现象是由众多的随机因素所引起的，每一个因素在总的变化里起着不显著的作用，那么就可以推断描述这个随机现象的随机变量近似地服从正态分布.由于这些情况很普遍，所以有相当多一类随机变量服从正态分布，从而正态分布成为概率统计中的重要分布.

【例1】一生产线生产的产品成箱包装，每箱质量随机，假设每箱平均质量为50 kg，标准差为5 kg，现随机抽取100箱进行称重，试求100箱产品质量大于5.1 t的概率.

解 设第i箱产品的质量为X（i单位：kg），（i=1，2，…，100），由题意知X1，X2，…，X100相互独立，于是一箱产品的质量为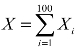，且E（Xi）=50，D（Xi）=σ2=52=25，则

根据中心极限定理，得

所以，100箱产品质量大于5.1 t的概率为0.0228.