随机变量函数的概率分布：离散型与连续型的计算方法

1.离散型随机变量函数的分布

已知离散型随机变量X的概率分布为

随机变量X的函数为Y=f（X），则函数Y的概率分布为

注意：当不同随机变量对应相同的函数值时，函数Y的概率分布中相同函数值只取一次，对应的概率求和.

【例15】随机变量X的概率分布为

求：（1）Y=2X+1的概率分布；（2）Y=X2的概率分布.

解 （1）当Y=2X+1时，有

所以，Y=2X+1的概率分布为

（2）当Y=X2时，有

所以，Y =X2的概率分布为

一般地，离散型随机变量X的函数Y（Y=f（X））的概率分布为

所以，Y=f（x）的概率分布为

注意：当i≠j，且存在yi=yj 时，将相等的y值所对应的概率相加.

2.连续型随机变量函数的分布

对于一般连续函数，可以根据其单调区间逐段讨论.下面讨论Y=f（X）的单调情形.

设X是连续型随机变量，其概率密度为px （x）.Y=f（X）是X的函数，其概率密度为py （y），有

y=f（x）的反函数为x=g（y），dx=g′（y）dy.

当y=f（x）为增函数时，有

根据概率密度的定义，有

同理，当y=f（x）为减函数时，有

【例16】已知连续型随机变量X的概率密度为(www.xing528.com)

求Y=X2的概率密度py （y）.

习 题 3.2

1.某产品有一等品、二等品、三等品和废品4个等级，其中一等品、二等品、三等品和废品所占比例分别为60%、10%、20%和10%.任取一个产品检查质量，用随机变量X描述这一试验，写出X的概率分布.

2.已知X的概率分布为

求：（1）a；（2）Y=X2-1的概率分布.

3.设一批产品共100只，其中有10只次品，从中取3次，每次任取1只，以X表示取出的3只中次品的只数，分别求出在以下两种情形下X的概率分布：（1）不放回抽样；（2）有放回抽样.

4.某汽车沿街道行驶，需要经过3个设有红绿信号灯的路口.若设每个信号灯显示红绿两种信号灯的时间相等，且各个信号灯工作相互独立.以X表示该汽车首次遇到红灯前已通过的路口数，试写出X的概率分布.

5.设某城市在一周内发生交通事故的次数服从参数为0.3的泊松分布，求：（1）在一周内恰好发生2次交通事故的概率；（2）在一周内至少发生1次交通事故的概率.

6.某种产品的废品率为0.1，任取20件产品，初步检查已发现2件废品.问这20件产品中，废品不少于3件的概率.

7.抛掷4枚骰子，X为出现1点的骰子数，求X的概率分布及其分布函数.

8.一批产品20个，5个废品，任意抽取4个，求废品数不多于2个的概率.

9.随机变量X的概率密度为，-∞＜x ＜+∞，求：（1）常数k；（2）X的分布函数F（x）；（3）X落在区间（0，1）内的概率.

10.设连续型随机变量X～N（3，4），求：（1）P{2＜X≤5}；（2）；（3）常数C，使P{X≤C}=P{X＞C}.

11.设顾客在某银行窗口等待服务的时间X（以min计）服从指数分布，其概率密度为

求：（1）等待服务的时间在50～150 h之间的概率；（2）等待服务的时间少于100 h的概率.

12.设连续型随机变量X的概率密度为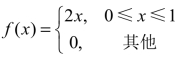，以Y表示对X的三次独立重复试验中“”出现的次数，试求概率P{Y=2}.

13.设X～N（10，22），求：（1）P{8＜X＜12}；（2）P{X＞12}；（3）

14.设X～N（10，22），已知，P{X＜b}=0.0668，分别求a和b.

15.某地区18岁女青年的血压为X（收缩压，以mmHg计），且X～N（110，122），试求该地区18岁女青年的血压在100～120 mmHg之间的可能性有多大.